Binary Search Trees

Overview

With this project, we will explore three different lessons involving binary search trees, and then as the pièce de résistance, a single implementation that successfully combines all three lessons.

We will start you with a basic implementation of a binary search tree to maintain a set of distinct values, supporting insertions, deletions, and searches. The three desired improvements are as follows:

● Split/Join: This complementary behaviors are used to split a single binary search tree into two different search trees containing respectively values less than or greater than a given parameter, or (re)combining two distinct binary search trees that are known to be less than and greater than some key value.

● Rank-based queries: By having each node maintain the size of its subtree, we can add support two additional queries, one that can tell you the rank of any existing key (i.e., the smallest key has rank 1, the second smallest has rank 2), and a second method that does the dual which is to find the key for a given rank (e.g. what is the third smallest key?)

● Treap balancing: By assigning each node an additional randomly-generated number, we can intentionally rebalance a search tree as a min-heap on those additional values. While this doesn't actually guarantee a balanced tree, it does remove the risk of imbalanced trees being dependent on the user's insertion order.

In later sections, we will further describe each of these tasks, as well as the challenges in simultaneously supporting them all in a single implementation.

odebase

We are providing a zip file, BST.zip, that contains a variety of files. Most notably, we are intentionally providing you with four different templates for your solution, because we did not want any potential problems with your final integration to stop you from being credited for success on each of the individual advancements.

● BST_join.py -- this file should be modified to provide working implementations of the split and join functions.

● BST_rank.py -- this file should be modified to provide working implementations of the rank-base methods keyToRank(key) and rankToKey(r).

● BST_treap.py -- this file should be modified to provide treap balancing. There are no new methods, but the existing implementations of insert and delete must be modified to ensure that the treap property is satisfied by the end of each operation.

● BST.py -- this file should be used for your final challenge of having a single implementation that provides all of the new features. While we expect you may borrow code from your other files to use in this file, there are some significant modification that will be necessary to combine all features.

● driver.py -- This is a driver that makes it easier for you to script a series of heap operations as a text file, including the additional validation/visualization. This is presumably the main file that you should execute for this project. More details on this below.

● inputs/ -- A few demonstration files to show input for the driver. While these are some good test cases, you should surely be developing many further tests of your own code (and I will be doing so for grading your code).

● cs1graphics.py -- our visualization is based on a python graphics package written here at SLU. Since non-standard package, I'm including it in this distribution.

Most important is understanding the expected data representation for the quake heap, and in particular how objects reference each other.

Binary Search Tree Representation

As a starting point, we are providing you with a working implementation of a generic binary search tree that supports insertions, deletions, and containment queries. We have chosen an abstraction of a TreeSet class which ensures that there are no duplicate keys within the tree; our given implementation is designed so that nothing is changed if it finds a "new" key already exists.

We have intentionally provided a very lightweight representation of a tree as a collection of nodes, with each node having a reference to its key and to its left child and right child (or None if no such child exists); additional _size field is added for the rank-based queries, and a _treap field is added to store a randomly-generated priority value for treaps. You are not to rename or add any other fields to the Node structures, as our testing/visualization depend on these fields.

One noteworthy issue of our design is that a node does not have a reference to its parent. While it may seem like a great convenience for nodes to have that information, doing so adds unwanted complexity to a search tree implementation.  It is not just that nodes use extra memory, but once you commit to maintaining parent pointers than every time you make a structural change to your tree, you have to make sure to properly update those pointers in a consistent way.  Later this semester, we will also explore another advanced topic and see additional drawbacks of maintaining parent pointers.

Of course, to implement most search tree functions, you often do need to navigate from a node to its parent.  Our solution to this is to temporarily build a list of nodes on the path from a root to a particular node of the tree while originally walking down to that node from the root. Since walking a path searching for a key is a basic part of almost all search tree operations, we have provided a nonpublic method, _tracePath(key), that performs the walk and which builds the list of nodes encountered on the search path. You should review our own use of that utility in the original implementation of methods look, insert, and delete.

Driver

We provide a driver that uses simple text commands to invoke various actions upon one or more trees. You can either interact with the driver manually by typing those commands, can have a text file prepared with commands and redirect that file to standard input, or give the name of the text file as a command line option when starting Python, in which case it will read input from that file rather than standard input.

The docstring at the top of the driver.py file provides an overview of all of the text-based commands that are accepted. One key issue is that to support testing of join and split, the driver need to be able to manage multiple trees. So all trees must be named with unique strings when using the driver. For example, you might create two trees named A and B and then each time you do an insertion you indicate which tree you wish to do (commands such as "I A 25" vs "I B 25" to insert key 25 into a tree). Then a command such as join can be used to combine A and B and a separating key, to form a new tree C (command such as "J A 30 B C"

Another key aspect is that you are doing different implementations in files BST_join.py, BST_rank.py, BST_treap.py, BST.py.  A single run of the driver must use one particular implementation for all trees and the driver requires that the very first command received be a single string that is either TJ, TR, TT, TA (shorthand for tree join, tree rank, tree treap, or tree all).

For convenience our driver also provide some basic validation testing and visualization of search trees (using our cs1graphics module).  Please see the documentation at the beginning of the driver as well as the sample inputs provided in the codebase. Note well that the internal validation is setup to only test the functionality expected by the above TJ/TR/TT/TA indicators. For all four, it will verify that a tree satisfies the binary search tree property, in that keys in a left subtree of a node must all have keys less than that of the node.  But if you are doing an implementation that supports the rank-based queries, then it also validates whether your stored _size field for a node accurately accounts for the size of the subtree rooted at that node, and similar if implementing a treap that the treap property is satisfied.  Note that the testing/visualization can only operate on a single tree at a time (using the aforementioned names for the trees).

Advice: split/join

In the basic version, the join function is by far the easiest of the two. You are given a new key and two trees, with the first tree known to have keys less than the given key, and the second tree known to have keys greater than the given key. (Note: our software does not check this condition, so it is up to the user to make sure not to join trees that violate the condition.)  So a join creates a new tree with a root node to hold the newest key, and that node's left and right children should be the roots of the two given trees.   This should run in constant time, as the new tree is essentially stealing the internal structures of the two originals; for the sake of consistency in the object-oriented framework, the roots of the two original trees should be reset to None so that those tree instances can no longer be used to make modifications to the structure of the join.

The split function will take more care. The key is to examine the search path for the given key (which may or may not be an element of the tree), and then to cut and paste pieces back together depending on which portions are found to be less than or equal to the key, and which are strictly greater.  There are lots of possible scenarios to consider, so be careful and do lots of testing.

Advice: rank-based query

The first task is to augment the basic tree in order to have each node maintain a _size field that is the total number of nodes (including itself) in its subtree.  For a basic search tree, notice that when a (non-duplicative) insertion occurs, the newly created node becomes a new descendent of all nodes on the search path, so all of their sizes must be updated.   Deletions are slightly more complicated, because of our replacement strategy when deleting a node with two children. But once the location of the actual node that is to be deleted from the tree structure is found, then all of its ancestors have their subtree size reduced by one.

Once you are confident that your tree nodes are accurately maintaining their subtree sizes, then you can approach the logic of the rankToKey and KeyToRank functions.  In both cases, as you traverse a search path, you can look at the sizes of the left and right subtrees of each node and should be able to determine precisely how many total nodes are left of (thus less than) a particular key and how many are right of (thus greater than) a particular key.  For example, if you are trying to find the key with rank 10 and the root of the tree has six nodes in its left subtree, and thus has rank seven itself, than clearly the node with rank 10 must be in the right subtree of the root (and in fact the third smallest node in that subtree).

Advice: treaps

Our starter code for the Node constructor for treaps creates a floating-point field, _treap, as a uniformly random number in range [0,1).

To perform an insertion on a treap, first allow the generic version of insert to do its job in adding a new node in the proper search tree location.  The only challenge once that is done is that the new node may have a treap value that is less than its parent, and in that case you must perform a tree rotation to make that node become the parent of its current parent (while making sure to properly keep the rest of the search tree valid).  This "upheap bubbling" must continue until the new node either reaches a location in which it has a parent with lesser treap value, or until it becomes the root of the tree.

For deletions, notice that deleting a leaf will not create any treap violation because no new child/parent relationships are formed. Similarly, our approach for deleting a node with one child essentially cuts that child out of the path, but its parent was already known to have smaller treap value than its surviving child, and so the treap property remains intact.  The only challenging case is when a node with two children is removed.  Our existing code base chooses to locate the successor of the node to be deleted and than effectively "moves" that entry to the location in the tree of the element that was supposed to be deleted, and then remedies the removal of the node below.  However, to properly implement a treap, the "moved" element's treap value should also move and the problem is that it now might be in an illegal location.

As an example (taken from input/basicTestTreap.txt), consider the state of the following treap just before we delete key 45.

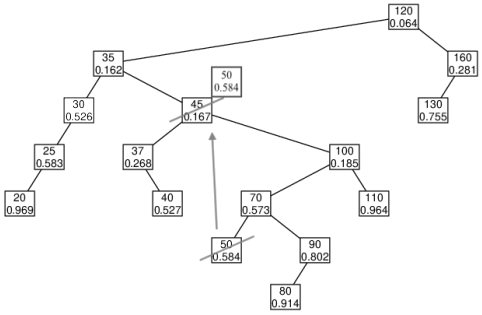
Given that the node with 45 has two, our deletion implementation finds the successor (that storing key 50), and effectively "moves" the 50 element to where 45 is currently, and then deletes the node that had been holding 50.  Deleting that other node is quite easy, but the element with 50 had treap value 0.584 and that should stay with the element yet we cannot leave that treap value where 45 used to be because that is larger than the treap values of its children (namely the 0.268 held by 37 and 0.185 held by 100).  Therefore we must "bubble" the node downward, and in particular we want to promote the node with value 100 because it has the smaller of the two children's treap values and thus is allowed to be the parent of 37.  So we "rotate" the edge between the new 50 and 100 so that 100 becomes the right child of 35, 50 becomes the LEFT child of 100.  Note that the subtree rooted at 70 gets moved in this transition, becoming the new right child of the node storing 50 (notice it is in the search tree location for keys that are smaller than 100 but greater than 50).

However, this process continues, as the new location of 50 still has a treap value 0.584 that is larger than both of its new children (the 0.268 held by 37 and the 0.573 held by 70).  In this case, another rotation must take place, this time with the left child 37 that has the smaller treap value.  If all goes well in this example, you will eventually reach the following treap.

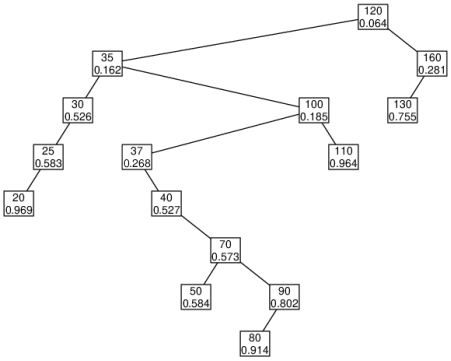
Advice: combining all features

Even more care will be needed when you try to combine the above functionality into a single implementation.

● For example, while it was great to implement split and join, if you are also trying to support the rank-based queries, you must make sure that you accurately maintained all subtree sizes while doing the reconstruction involved in a split or join operation.

● For a treap, even after the standard form of an insertion or deletion and the change that causes to subtrees on the path, any further rotations that are used to restructure the tree will impact the size of subtrees along the path.  So it is necessary to recompute all the subtree sizes for impacted nodes, but you still want this implementation to run in time proportional to the path height, so you can't actually afford to traverse all of those subtrees; you must infer the new sizes only for those nodes who's children were changed.

● It turns out that combining "split" with treaps is actually quite trivial because if you look at the natural algorithm for how you glued pieces of the split path back together, you should find that things that used to be below a node due to a treap value will remain below such a node even after you put the pieces back together. So this is good news in that you shouldn't have to update the split code to maintain the treap property.
But unfortunately, the join function does become more complicated with treaps.  In the generic version, a join was easy because you just make the new key the root and repurpose the existing two trees to form the left and right subtrees.  But for treaps, that newly created root node has a randomly selected treap value and that value might not compare well to those of its children.  In particular, if it is larger than either of its children, you must preform the downward bubbling process (akin to the one used in the special case of deletion).

We hope that you will be able to use much of the code from your earlier implementations in the final BST.py implementation, but some significant refactoring will be warranted.  So this is why we are having you still submit (hopefully working) versions of those other three implementations to get credit for your successes, and to make this final combined implementation its own file.

Examples and Illustrations

Our codebase includes an inputs/ folder that provides several interesting test cases that can be used with our driver.  Rather than clutter this page with lots and lots of discussion and illustrations, we will provide additional illustrations as a separate page.

The assignment is worth 50 points, apportioned as follows:

● The split and join methods (BST_join.py)

● The rank-based methods (BST_rank.py)

●  The treap balancing (BST_treap.py)

●  Successful integration of all three (BST.py)