STA447/2006S: Stochastic Processes Winter 2021

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

STA447/2006S: Stochastic Processes

Winter 2021

Midterm Exam 1

Problems:

1.  (5 pts) Consider a Markov chain defined on 5 = s1, 2, 3} and

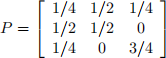
(a)  (1 pt) Let X0 = 1. What is 玲(X1 = 3)?

(b)  (1 pt) Let T之 = infsn 2 1 : Xn = i}. Compute E(T|IX0 = 1) by conditioning on X| .

(c)  (2 pts) The following statement is true:

If 5 is finite and     ieS pij  = 1 for all j e 5 , then πi  = 1/I5I for i e 5 is a stationary

distribution.

Using this result, compute E(T之IX0 = i) for i = 1, 2, 3.

(d)  (1 pt) Does the statement in (c) hold when I5I = o? If yes, prove it. If no, provide a counterexample.

2.  (6 pts) Determine if there exists a Markov chain that satisfies the following conditions. If it exists, provide an example. If not, explain why.

(a)  (1 pt) A Markov chain has i, j e 5 with 0 < f之_  < 1 and p之(L)_(n)ò = 0 for all n 2 3.

(b)  (1 pt) A Markov chain is irreducible and and has a transient state, and there are i, j e 5 with p之(L)_(n)ò 2 1/5 for all n e N.

(c)  (1 pt) A Markov chain is irreducible, has one state i with p之(L)之(n)ò  < o, and is

reversible with respect to some probability distribution π .

(d)  (2 pt) A Markov chain with transition probability matrix  P  is irreducible,  but a Markov chain with transition matrix Q = P1  is reducible.

(e)  (1 pt) A Markov chain has a unique stationary distribution but is reducible.

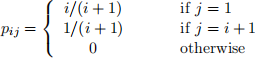
(a)  (1 pt) Write down the transition probability matrix.

(b)  (1 pt) Compute the period of state 3 using the definition of the period.

(c)  (1 pt) Is this chain irreducible? Why or why not?

(d)  (2 pts) Find a stationary distribution π for this Markov chain. Is it unique? Why or why not? Hint: Use

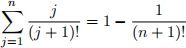
(e)  (1 pt) Classify the states in this chain into one of the followings:  (i) null recurrent,

(ii) positive recurrent, or (iii) transient. State your reasoning.

(f)  (1 pt) Is this chain reversible with π? Why or why not?

(g)  (2 pt) Propose a Metropolis algorithm to generate a random variable from the sta- tionary distribution π . Be sure to illustrate in detail.

(h)  (1 pt) What is the expected value and variance of this distribution π?

4.  (6 pts) A box contains N balls with some blue balls and some red balls (note: it is possible that all balls are both red or both blue).  At each stage, a coin having probability p of landing heads is flipped. Once a head appears, a ball from the box is chosen and is replaced by a blue ball. If a tail appears, a ball from the box is chosen and replaced by a red ball. Let Xn be the number of blue balls in the box after the nth flip.  (5 = s0, 1, 2, . . . , N })

(a)  (1 pt) Compute p之_  for j e 5 .

(b)  (1 pt) Which states are recurrent and which states are transient? Be sure to provide appropriate reasoning for your answer.

(c)  (2 pts) Show that a stationary distribution π is

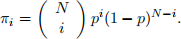
(d)  (2 pts) What is limnoo 玲(Xn = 1)? Show your reasoning.

5.  (3 pts) Provide at least one suggestions that could improve the quality of this course in the future. No point will be given for responses saying that everything’s good.