MAT 6470/6473. TP2 : L’orbite d’une comète.

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAT 6470/6473. TP2 : L’orbite d’une comète.

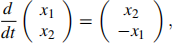
avec condition initiale

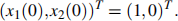
(a) Trouvez la solution exacte zex(t）de (1)-(2).     (2 points)

(b) Résolvez (1)-(2) sur l’intervalle de temps (0← 1| en utilisant RK4 avec h = 1/n où n = 2 ← 4 ←．．．← 210.     (2 points)

(c) Produisez un graphique loglog de la norme 2 du vecteur erreur vs. h et déterminez l’ordre de convergence vers la solution zex(1）.     (2 points)

2. Les composantes r1 (t）et r2 (t）du vecteur position r(t）du centre de masse d’une comète qui se meut autour du soleil satisfont aux équations de mouvement adimensionnelles

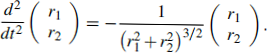
On va toujours supposer que, à t = 0, r1 = 10, r2= 0, r˙ 1 = 0 et r˙2 = v0 pour une certaine vitesse scalaire v0. Si v0 n’est pas trop grande, le centre de masse de la comète trace une ellipse dans le plan, avec le soleil situé en un des foyers de l’ellipse (première loi de Kepler). La forme de l’ellipse dépend de la valeur de v0 . La période de l’orbite, P(v0）, est le premier temps pour lequel r(P）= r(0）et r˙ (P）= r˙ (0）.

Pour les questions 2(b) et (c) ci-dessous

( on pose t0 = 0 et tf = 10 pour le calcul de hmax (voir la page 392 de Fortin [1]),               ( on utilise une estimation de l’erreur égale à norm(E,’inf’) où E est l’erreur obtenue de

(7.13) de Fortin [1],

( on choisit une précision tol (voir la page 392 de Fortin [1]) égale à 1 女 10!6

(a) Écrivez le système d’equations (3) comme un système de 4 équations du premier ordre. (2 points)

(b) Utilisez la méthode adaptative de Runge-Kutta-Fehlman (RKF) pour calculer les périodes P(v0）pour v0 = 0.02:0.02:0.1 (selon la notation MATLAB). Notez qu’il ne faut pas que vous attendiez à ce qu’on revienne précisement au même endroit après une période. Sug- gestion: calculez P(v0）en utilisant une interpolation linéaire des temps tj et tj＋1 où ces derniers sont définis comme étant les plus petites valeurs discrètes de t telles que r2 (tj）< 0 et r2 (tj＋1）; 0. Créez un graphique de1P(v0）vs. v0 .           (4 points)

(c) Soit v0 = 0．1. Utilisez la méthode RKF pour produire un graphique montrant r1 et h (le pas du temps adaptatif) contre le temps t è「0← P(v0）|. Commentez ces résultats. Notez par N(v0）= j＋1 le nombre minimal de pas de temps (voir (b) ci-dessus) nécessaire pour faire au moins un tour complet et calculez le pourcentage erreur relative 100% 女 (r1 (P(v0））! 10）/10. (N.B. r1(P(v0））doit être calculé par interpolation).                             (3 points)

(d) Soit v0  = 0．1.  Utilisez RK4 avec N(v0）pas uniformes de longueur h = P(v0）/N(v0） pour essayer de refaire les calculs de la trajectoire de la comète. Produisez un graphique montrant les trajectoires obtenues en (c) avec RKF et, avec le même nombre de pas, les trajectoires obtenues avec RK4. Commentez vos résultats.                                (2 points)

(e) Lorsqu’on utilise RK4 avec v0 = 0．1, combien de pas de temps uniformes a-t-on besoin au minimum pour obtenir une erreur relative 100% 女 (r1 (P(v0））! 10）/10 plus petite que celle obtenue en (c)? Commentez. Produisez un graphique de la trajectoire de la comète obtenue avec RK4 dans ce cas-ci.                                                                     (3 points)