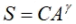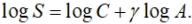STAT*2050 Statistics II Winter 2022

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

STAT*2050 Statistics II

Winter 2022

Assignment #1

Note: There may be parts of this assignment that will not be graded, but it is in your best interests to do all questions. The graded components will be submitted via Crowdmark; you will receive a template for submitting your answers in your email. Further instructions on Crowdmark as well as various hints for completing this assignment will be forthcoming.

1. The statistician Francis Anscombe constructed a set of four data sets that show very similar statistics when a regression and correlation analysis is conducted, but look very different when graphed. The data sets are stored in a single file called “Anscombe correlation data sets” on our course website. The first three data sets have the same X values (labelled “X1to3"). Conduct simple linear regression and correlation analyses using R on the four data sets and compare (i) the least squares regression equations, (ii) the coefficients of determination and correlation coefficients, and (iii) the ANOVA tables. Also graph the four data sets. Note: The Anscombe data sets are in our text, Regression Analysis by Example (4th ed.) by Chatterjee and Hadi 2006); see pp. 25! 26. [We will select certain info that you should obtain from your analyses for you to hand in.]

2. The Galapagos Islands data set that you will use for this assignment is posted on our course website. The original data set came from “Data” by Andrews and Herzberg (1985). A few missing values for Elevation have been filled in thanks to Julian Faraway. Island areas have been updated according to values provided by Bernsted-Smith (ed., 1999, “A Biodiversity Vision for the Galapagos Islands”. The variables for the 30 islands are: Record Number (Record), Island, Number of observed species (NoSpp), Number of native species (NativeSpp), Area in hectares (Area_ha; convert this to Area in km2 ), Elevation in m, Distance from nearest island in km (NearestIsland), Distance from Santa Cruz in km (SantaCruz), Area of adjacent island in km2 (AreaAdjacent).

In this assignment we’ll look at the relationship between the number of species and the area of the island. This is a fundamental relationship in the Theory of Island Biogeography, which models how species numbers increase with increased island area. If S is the number of species and A is the area of the island, then

where C is a constant and ã is a “biologically meaningful” parameter. We can convert this to a pseudolinear model by taking logs on both sides:

For theoretical reasons, then, we can expect log transforming both the area and the number of species will do a good job of linearizing the relationship (although it really doesn’t matter which base of log we use, we’ll use base 10 logs here for consistency). However, we’ll start off “naive” about the Theory of Island Biogeography and try a couple of other plots first.

(a) First try graphing a linear regression of NoSpp on Area. The fit is truly awful. Why?

(b) The results in (a) would suggest that at the very least the variable Area needs to be transformed. Graph a regression of NoSpp on log10 (Area). Obtain the coefficient of determination (r2) for this fit. You should note this fit is substantially better than in (a) but still leaves much to be desired. What shortcomings do you see in the fit of the linear model here?

(c) Now try a fit of log10 (NoSpp) on log10 (Area). You should find this fit quite aesthetically pleasing! Perform a regression analysis for this fitted model.

(d) What is the estimated linear regression equation for the model in (c)?

(e) Obtain (individual) 95% confidence intervals for the intercept and slope parameters.

(f) Use the results in (e) to obtain 95% confidence intervals for ã and C.

(g) Plot log10 (NoSpp) versus log10 (AreaAdjacent). Is there a statistically significant (at the 5% level) linear relationship here

(h) Obtain the Pearson correlation coefficient between (i) NoSpp and Area (in km2 ) and (ii) log10 (NoSpp) on log10 (Area). Comment on the values you obtain.

(i) Obtain the Spearman correlation coefficient between (i) NoSpp and Area (in km2) and (ii) log10 (NoSpp) on log10 (Area). Comment on the values you obtain.

(j) Briefly explain how the Pearson and Spearman correlation coefficients differ.

3. In a certain study in which a simple linear regression and correlation analysis was conducted, a correlation coefficient of r = 0.57 was calculated on 19 observations.

(a) What would be the value of the F test statistic for testing H0 : â1 = 0 versus H1 : â1 … 0?

(b) What would the p-value be for the F statistic calculated in (a)?

(c) Would the null hypothesis be rejected at the 5% level of significance? Why or why not?

4. In this exercise you will analyze a subset of a “green brain” data set I compiled in Fall 2019. The data set will be explained further in class, but for now it is sufficient to state that the data set you will work with here consists of wet weight and dry weight measurements (in grams) for 50 “green brains” (fruits of the osage orange tree). Measuring a wet weight is easy whereas measuring a dry weight requires heating the green brains in a drying oven for a considerable time, so we will treat wet weight as the predictor variable and dry weight as the response variable.

(a) Plot the scattergram of dry weight on wet weight, and superimpose the estimated simple linear regression equation. (This will get you started but you won’t hand this in.)

(b) Specify the simple linear regression model (model equation plus model assumptions) that you will base subsequent statistical inference on.

(c) Obtain 95% (individual) confidence intervals for the intercept and slope parameters.

(d) Test the null hypotheses that each of the intercept and slope parameters is equal to 0; use a two-sided alternative hypothesis for each test. These tests are conducted on your R output; you simply need to identify the appropriate test statistic values and interpret the associated p-values. Use a 5% level of significance.

(e) In many situations where a simple linear regression analysis is conducted, the test that the slope parameter is equal to 0 is of much greater interest than the test that the intercept is equal to 0. For our data set, it can be argued that the reverse is true; that is, testing if the intercept parameter is equal to 0 is of much greater interest than testing if the slope parameter is equal to 0. Briefly summarize the key points to this argument.

(f) Briefly explain (i) why a one-sided test for the slope parameter would have been more sensible than the two-sided test conducted by R (more sensible does not mean it was really that sensible), and (ii) why the 95% confidence interval for the slope parameter provides more useful information than the corresponding hypothesis test.

(g) In certain cases an argument can be made for forcing the fitted regression equation to pass through the origin. A good discussion on this topic, and how to do so in R, is available at:

https://rpubs.com/aaronsc32/regression-through-the-origin

What evidence do you have that fitting a regression equation to pass through the origin might be a good thing to do with the “green brain” data? Obtain this regression equation for our data.

(i) Superimpose the regression equation of (g) to your graph in (a). Label your graph properly and include a legend for the two equations. Hand this graph in. [This is most easily submitted to Crowdmark as a separate pdf file.]

(j) In the future we will look at a formal test for comparing the two models fit. At this point, though, we will ask, what evidence do you have that the SLR equation that included an estimated Y-intercept is not much better than the SLR equation that is forced through the origin? [Note: the multiple R2 is not a useful measure here!]