MTH771P / MTH771U Foundations of Mathematical Modelling in Finance (2021/22)

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

1. Suppose that I throw two unbiased dice, scoring values X and Y .

Let S be the sum of these values (S = X + Y) and M  be the lesser of these values (M = min(X, Y)).

(a)  Calculate the expectations of S and M .

(b)  Calculate the (conditional) expectation of S given M .

(c) Are S and M independent? Justify your answer.

2. A continuous random variable X has the probability density function

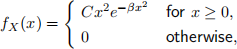
where β > 0 is a constant, and C is the normalisation constant.

(a) Sketch the probability density function and cumulative distribution function of X . (b)  Find an expression for the normalisation constant C, expressed in terms of β .

(c)  Calculate the expectation and the variance of X .

(d)  Finally, determine the probability density function of the random variable Y = X + k , where k is some constant.

3. At the start of each year in a nine-year period, I deposit a random amount Wi  (i = 1, . . . , 9) into a bank account, where the Wi  are independent, and each Wi  is distributed as follows:

The annual interest rate is R , and interest is paid at the end of each year, and is reinvested. I make no withdrawals during the nine-year period, and so all my money remains invested until the end of the ninth year.  Let B  be my balance at the end of the ninth year, including the final interest payment.

Find a compact formula for the expected value of B .

4. Suppose that, at some time t, you construct a portfolio containing the following financial instruments: (i) A short position in a share of company X, (ii) a long position in a European call option on X, and (iii) a short position in a European put option on X. The two options have the same strike price K and the same expiry time T (where T > t).

You may assume that the share pays no dividends between times t and T , and that all market participants have access to a bank account with continuously-compounded interest rate r per year.

(a)  Determine the value of this portfolio at time T as a function of the share price ST at that time.

(b) Assuming that no arbitrage opportunities exist in the market, derive an expression for the value of the portfolio at time t.

Note: Be sure to justify your answer fully.

(c)  Hence, derive the put-call parity relationship for European options.

5.  Consider the one-period binomial model for option pricing. The price of the underlying share at time 0 is S(, and it can move either up to S）(．)u尸  or down to S）(．)d尸  at time 1. There is also a bank account that pays interest at the rate R per period.

You may assume that there are no arbitrage opportunities in the market.

(a) Working from first principles, derive a formula for the value F(  at time 0 of a forward

contract on the share, with delivery (strike) price K and delivery (expiry) time 1.

(b) Suppose that you buy 1000 of these forward contracts at time 0. How many shares would you need to buy or sell, also at time 0, in order to make your position risk-free?