Math/CS 467 Final project

发布时间：2021-12-11

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Math/CS 467

Final project

The goal of the ﬁnal project is to implement the quadratic sieve algorithm for factoriza- tion. I have outlined the various parts below.

Your ﬁnal submission will be similar to a homework submission, except this time I will be looking closer at the code. Many of the parts simply require you to implement something, and others ask you to test out or interpret what you have implemented.

You may talk to me or each other about the code you are writing. However, you may not look at each others’ code (or code from elsewhere) as you are implementing these programs. The one exception is that you can use pseudocode from the book, and in the case of rref, you can use pseudocode from the internet.

Good luck!

Problem 1. The ﬁrst part of the implementation is to write some preliminaries useful later.

a) We’re often going to need to use some form of trial division. Write a function that given a number n and a list of primes p1 , . . . , pr computes a factorization

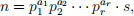
where gcd(pi , s) = 1. The function should return the vector [a1 , . . . , ar ] and the number s (formatted however you want).

For example, when we have a list containing only the prime 2, this function should write n = 2a s where s is odd. You can use this in Tonelli’s algorithm and the strong pseudoprime test.

b) Before plugging a number into the quadratic sieve, you should probably check that it is not prime. Implement the strong pseudoprime test. (You can recycle some code here: you wrote fast exponentiation on a previous homework, and to write a number in the form 2s . t you can use your function from (a) with the single prime p1 = 2.)

c) SUBMIT: Is the number 3004879 likely to be prime? Justify your answer by explaining what your program has discovered.

Problem 2. Now a couple more preliminaries.

a) Implement an algorithm to compute the inverse of a modulo n. (You need this in Tonelli’s algorithm.) Hint: this uses the extended Euclidean algorithm, which you implemented on an early homework assignment.

b) SUBMIT: Compute the multiplicative inverse of 1163 modulo 1999.

c) Implement Tonelli’s algorithm for ﬁnding a square root modulo p.

d) SUBMIT: Find a square root of 117 modulo 3691. What values did you get for the ik in Tonelli’s algorithm? (If you used another algorithm, give me the values of the parameters you computed there.)

Problem 3. We will need some linear algebra tools available to us.

a) Implement Gaussian elimination modulo 2. Given a matrix M , compute rref(M). (In class we looked at the pseudocode from gttpsp::an/whkhpadha/orf:whkh:Row aXgalon eorm.PsaudoXoda eor raduXad row aXgalon eorm. It’s ﬁne if you want to consult that.)

b) Given a set of vectors v1 , . . . , vr , ﬁnd all combinations a1v1 + . . . ar vr that are equal to 0. Your implementation should give a complete set of independent solutions. (If you know what it means, I went a basis for the space of solutions.)

c) SUBMIT: I have attached a list of 10 binary vectors of length 8. Find two independent ways to write the zero vector as a linear combination of these vectors.

Problem 4. Now it’s time to generate the factor base.

a) Given a bound B , create a list of all primes less than B .

b) Now given B and n (the number to be factored), generate a list of all primes less than B with ╱、= 1.

c) SUBMIT: Give me a list of all primes less than 200 with ╱、= 1.

Problem 5. Next, we need to actually run the sieve. Suppose that n (the number to be factored) and B (the upper bound on the primes), and M (the number of r’s to sieve) are given.

a) For all values of r from [rnl to [rnl + M, compute s(r) = log(r2 _ n). Store these in an array.

b) Generate a factor base as in the previous problem. For each prime p in the factor base, ﬁnd a solution t2 三 n (mod p).

c) SUBMIT: Say you want to factor n = 7386829. Take B = 1000. What is your factor base? Give t that works for each prime in your factor base.

d) Now run the sieve. For each r such that r2 _ n is divisible by p, subtract log p from the corresponding entry of the list. Do this for every p.

e) Now you can read oﬀ the values of r for which r2 (mod n) is B-smooth (i.e. splits into primes that appear in our factor base.) Look for entries in your list where the remaining value is very close to 0. For each of those, use the trial division program from 1(a) to try to split it into factors completely. Save the results as the columns of a matrix.

f) SUBMIT: Keep the same factor base and n as above. Can you ﬁnd enough values of r to get a factorization? Give me your values of r, with the corresponding factorization of f(r).

Problem 6. At last, put it all together. Suppose that n is the number to be factored.

a) Before starting the algorithm, check that the number passes the strong pseudoprime test for some base.

b) Now choose B and generate a factor base. For each factor in the factor base, solve t2 三 n (mod p).

c) Run the sieve: ﬁnd many values of r such that r2 (mod n) factors over our factor base.

d) Use Gaussian elimination to ﬁnd a product of these r’s that is a perfect square. Use this to ﬁnd a factor of n.

e) SUBMIT: Let’s try this for a more serious number. Take n = 10378625636772128629. Tell me the B you want to use and the number of primes in the factor base you compute. How many r values do you need before you are able to ﬁnd a dependence? What are the x and y values you end up with that satisfy x2 三 y2 (mod n). What is the resulting factorization?

f) In the course of the previous example, you needed to make a few choices for parameters like B , M, the sieving threshhold, etc. Tell me what values you used, and how you arrived at them.