ECON0060 Problem Set 3

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

ECON0060

Problem Set 3

You do not need to hand in your solutions, they will not be graded.

Question 1

Consider the linear panel AR(1) model

yit = yi,t−1 β + αi + εit,                 for t = 2, . . . , T,

yi1 = αi + εi1,                               for t = 1.

where i = 1, . . . , n. We assume that 0 < β < 1, the shocks εit are independently dis-tributed across both i and t with ❊(εit) = 0 and ❊(ε 2 it) = σε 2 , and αi is distributed independently from all εit.

(a) Write down the within group estimator βˆWG for this model.

(b) Show that the probability limit of βˆWG is smaller or equal than the true parameter β, i.e. show that as n → ∞ we have βˆWG →p β∞ WG where β∞ WG ≤ β.

(c) Assume you observe a sample yit over T = 3 time periods and n = 100.000 individ-uals that is generated from the above model. You calculate βˆWG = 0.36 for your sample. Would you feel comfortable to conclude that the true value satisfies β > 0?

Question 2

Consider a dynamic panel data model with a lagged dependent variable, and one addi-tional regressor wit, namely

yit = yi,t−1 β1 + wit β2 + αi + εit,

    = xit β + αi + εit,

where xit = (yi,t−1, wit) and β = (β1, β2)'. We observe yit and xit for i = 1, . . . , n, and t = 1, 2, i.e. yi0 is also observed. We assume that yi0 = αi + εi0, and that εi0, εi1, εi2, wi1, wi2, and αi are mutually independent, iid across i, and are all normally distributed with mean zero and variance one. First differences are defined by ∆yit = yit − yi,t−1, ∆wit = wit − wi,t−1, ∆xit = xit − xi,t−1, and ∆εit = εit − εi,t−1. Define zi = (∆wi2, yi0). Consider the following estimators for β

The first estimator is the OLS estimator of the original model, the second estimator is the OLS estimator after first differencing, and the third estimator is the IV (or 2SLS) estimator after first differencing, using zi as instruments.

(a) Calculate E [wit (αi + εit)] and E [yi,t−1 (αi + εit)] for t = 1, 2.

(b) Is βˆOLS a consistent estimator for β? Briefly discuss which consistency conditions are satisfied or violated. You can use your result in (a).

(c) Calculate E(∆wi2 ∆εi2) and E(∆yi1 ∆εi2).

(d) Is βˆFD−OLS a consistent estimator for β? Briefly discuss which consistency conditions are satisfied or violated. You can use your result in (c).

(e) Calculate E(yi0 ∆εi2). Furthermore, calculate the determinant of the 2 × 2 matrix E(z'i∆xi2). Is this matrix invertible?

(f) For what values of β1 is βˆFD−IV a consistent estimator for β? You can use your result in (e). Prove that βˆ FD−IV is consistent for those values of β1.

(g) We now change the initial conditions to yi0 = εi0, but otherwise the above assump-tions are unchanged. Now, for what values of β1 is βˆ FD−IV a consistent estimator for β?

Question 3

Consider the panel AR(1) model for T = 4 time periods,

yit = ρ yi,t−1 + αi + εit,         i = 1, . . . , n, t = 1, 2, 3, 4,

where ρ ∈ [0, 1) is an unknown parameter, and αi and εit are unobserved. We assume that εit ∼ iid N (0, σε 2 ), that is, εit is independent across i and over t. No assumptions are imposed on αi . We do not observe yi0, but we assume that yi0 is generated from an infinite past history of the AR(1) process, implying that yit is stationary. We observe an iid sample (yi1, yi2, yi3, yi4), i = 1, . . . , n. Let ∆yit = yit − yi,t−1 and ∆xit = xit − xi,t−1, and for ` = 1, 2, 3 consider the estimator

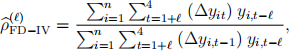
This is the IV estimator after first differencing, using the e-lagged outcome as an instru-ment.

(a) Assume 0 < ρ < 1. Which of the three estimators ρb (1)FD−IV, ρb (2)FD−IV, ρb (3)FD−IV is consistent for ρ? How does your answer change if ρ = 0? Explain your answer, but no consistency proof required.

Assume 0 < ρ < 1 for all of the following subquestions. In addition, for the following two subquestions (b) and (c) we make the simplifying assumption that αi = 0. In that case, one can show that E(yit) = 0, γ0 := E(y2it) = σε 2/(1−ρ 2 ), and γ` := E(yityi,t−` ) = ρ ` γ0 for ` ∈ {1, 2, 3, . . .}. You can use those results in the following.

(b) Show that that as n → ∞ we have 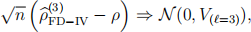 and derive a formula for V(` =3), which should only depend on ρ.

(c) What happens to V(` =3) as ρ → 1? Explain your finding.

Analogously to your derivation in (b) one can also show that 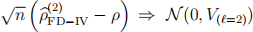 as n → ∞, but you do not need to derive this result.

(d) Without actually calculating V(e=2), would you expect V(e=2) to be larger or smaller than V(e=3) found in part (c)? Explain your answer.