关键词 > C语言代写
HW5
发布时间：2024-06-19
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Assignment
In this assignment, we use a message-passing interpretation of successive decoding of polar codes and density evolution techniques to get further insights into the decoding process and to determine the ordering of the bit channels. The encoder and decoder for a transmission of a length-4 polar code over a binary symmetric channel (BSC) with error probability ∈ are illustrated on Figure 1.
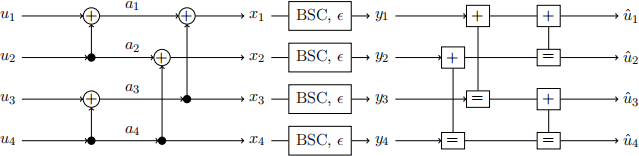
Figure 1: Encoding and decoding of a length-4 polar code and transmission over a BSC.
In Figure 1 on the left, 田 represents modulo-2 additions at the encoder. On the right, 田 represents the message passing decoder module at the decoder side for the corresponding modulo-2 summation at the encoder, and "= " represents the message passing decoder module at the decoder side for the corresponding equality constraints at the encoder. The message schedule for the different bit channels is illustrated in Figure 2(a)-(d), where messages are represented by the variable mi along the connections in the graph. In this assignment, we assume binary messages mi ∈ {0, 1} for simplicity, which allows us to derive the density evolution of the messages by calculating the error probabilities of the messages. Furthermore, the bit estimates ^(u)i equal the final messages mj (e.g., ^(u)1 = m10 and ^(u)2 = m12 ).
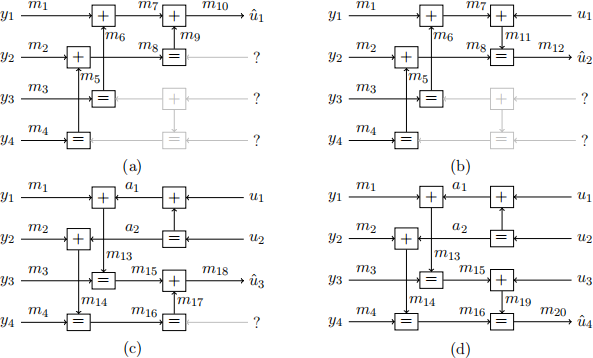
Figure 2: Message flow at the decoder during the four decoding steps of the successive decoder:
(a) decoding u1 given y1 , . . . , y4 ; (b) decoding u2 given y1 , . . . , y4 and u1 ; (c) decoding u3 given y1 , . . . , y4 and u1 , u2 ; (d) decoding u4 given y1 , . . . , y4 and u1 , . . . , u3 . The variables u1 , . . . , u4 and a1 , a2 correspond to the true bits at the encoder, and variables ^(u)i denote their estimates at the decoder.
Problem 1 [8 points]
We start with analyzing the decoder modules for a modulo-2 sum constraint and equality constraint, illustrated in Figure 3(a) and (b), respectively, with messages m1 , m2 , m3 corre- sponding to the decoder’s belief of the true bits x1 , x2 , x3 at the encoder, respectively, and the error probabilities ∈i = Pr(mi 
xi). Since we consider binary message passing, the outgoing message for the modulo-2 sum decoder is the modulo-2 sum of the incoming messages. For the equality constraint decoder, the outgoing message is chosen to equal the most reliable in- coming message (i.e., the one with the smaller error probability). If both messages are equally reliable but disagree, one is picked at random with equal probability.
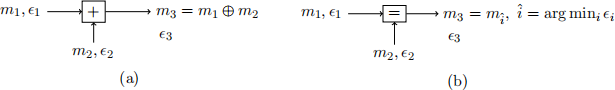
Figure 3: Decoders for modulo-2 sum constraint x3 = x1 田 x2 in (a) and equality constraint x1 = x2 = x3 in (b).
(a) Consider the decoder in Figure 3 (a) first: (3 points)
(i) Derive ∈3 as a function of ∈ 1 and ∈2 .
(ii) What happens to ∈3 if ∈2 = 0? What does it mean for a message m2 if ∈2 = 0, and what is the consequence for m3 ?
(iii) What happens to ∈3 if ∈2 = 0.5? What does it mean for a message m2 if ∈2 = 0.5, and what is the consequence for m3 ?
(b) Now consider the decoder in Figure 3 (b): (3 points)
(i) Derive ∈3 as a function of ∈ 1 and ∈2 .
(ii) What happens to ∈3 if ∈2 = 0? What is the consequence for m3 ? (iii) What happens to ∈3 if ∈2 = 0.5? What is the consequence for m3 ?
(c) Use the results from above to explain why we do not need to consider the grey-shaded parts of the decoder in the four decoding steps in Figure 2(a)–(d). Note that the ui on the right-hand side of the decoder are assumed to be the correct bits. (2 points)
Problem 2 [15 points]
In this problem, we use the results from the first problem to analyse the end-to-end error probabilities and capacities of the bit channels for the given implementation of the message passing decoder.
(a) Derive the messages m1 , . . . , m20 , and derive the error probabilities ∈ 1 , . . . , ∈20 as a function of the BSC error probability ∈ . (4 points)
(b) What is the ordering of the channels from the most reliable bit channel to the least reliable bit channel? Does the order vary with the channel parameter ∈ or is it the same regardless of ∈? (2 points)
(c) Derive the rates provided by the bit channels (i.e., the input-output mutual information) as a function of the channel error probability ∈, (3 points)
I1 = I(u1; m10) (1)
I2 = I(u2; m12) (2)
I3 = I(u3; m18) (3)
I4 = I(u4; m20) (4)
and prepare a plot that displays the rates I1 , . . . , I4 as function of ∈ ∈ [0, 0.5].
(d) Prepare a second plot that compares the sum rate IΣ = I1 + . . . + I4 to the overall capacity of the four BSCs, C4 = 4 · CBSC(∈), where CBSC(∈) denotes the capacity of a single BSC with error probability ∈ . What can you conclude from this plot? (2 points)
(e) In this part, we try to explain the observations made in Part (d). For an optimal decoder, we would expect (4 points)
I1 = I(u1; m10) = I(U1; Y1, . . . , Y4) (5)
I2 = I(u2; m12) = I(U2; Y1, . . . , Y4, U1) (6)
I3 = I(u3; m18) = I(U3; Y1, . . . , Y4, U1, U2) (7)
I4 = I(u4; m20) = I(U4; Y1, . . . , Y4, U1, . . . , U3) (8)
(i) Explain why an optimal decoder satisfies IΣ = C4 .
(ii) Explain why message passing with the optimal component decoders is optimal. (iii) Explain why the decoders introduced in Figure 3 are suboptimal.
(iv) An optimal decoder can be implemented with log-likelihood ratios as messages. What are then the optimal decoding functions for the two different types of com- ponent decoders?
Problem 3 [6 points]
In Problem 2(d), we have shown that the order of the bit channels is independent of the channel quality for that specific channel and the given suboptimal decoder (i.e., if channel i is the most reliable channel, then it will be the most reliable channel for all choices of the channel parameter). This observation generalises to the optimal decoder and to so called degraded channels in the sense that the set of frozen bit channels (i.e., the set of unreliable channels whose input is set to a constant value) for a better channel quality is always a subset of the frozen set for the degraded channel with lower quality. This nesting of the frozen sets is illustrated in Figure 4 where we assume that the order of bit channels from the best bit channel to the worst is u1 , u2 , u3 , u4 . The frozen bits are highlighted in blue, and the reliable bit channels are displayed without any color.
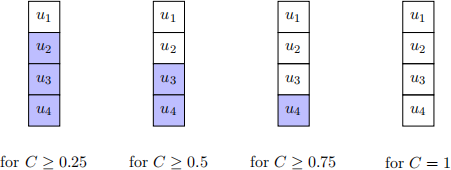
Figure 4: Illustration of the nesting of the frozen sets (in blue) as the channel quality increases.
This nesting property can be utilised to implement an automatic repeat request (ARQ) scheme with incremental redundancy for channels with constant but unknown channel quality (e.g., slow fading channels where sequences of code blocks experience the same channel capacity), by chaining codewords together. The beginning of such a chaining construction is shown in Figure 5. The first block assumes C = 1 and allocates information bits b1 , . . . , b4 to all bit channels. If the transmission fails, it must be that C < 1, and the second block is transmitted with frozen bit u4 = 0. This block will bedecodable if C ≥ 0.75. To ensure that the first block can be decoded under this condition (i.e., for C ≥ 0.75), the second block repeats the last bit b4 , which can then be used as a frozen bit u4 = b4 when decoding the first block (this is known as chaining). The remaining bit channels u2 and u3 are used to transmit new information bits b5 and b6 in the 2. block, and the overall rate after two blocks is R2 = 6/8 = 3/4. If decoding fails since C < 0.75, the chaining constructions is successively extended to the 3. block and to the 4.-6. block if necessary.
(a) We now extend the chaining construction to the third block. (3 points)
(i) Which capacity do we need to be able to decode the third block?
(ii) Which additional frozen bits do we need to decode the first two blocks, and what is then your choice for the bits u1 and u2 in the third block?
(iii) What is the overall rate after three blocks and how does it compare to the capacity requirement for successful decoding?
(b) We now analyse the situation for the last three blocks. (3 points)
(i) Which capacity do we need to be able to decode the last three blocks?
(ii) Which additional frozen bits do we need to decode the first three blocks and should be transmitted in the last three blocks?
(iii) What is the overall rate after six blocks and how does it compare to the capacity requirement for successful decoding?
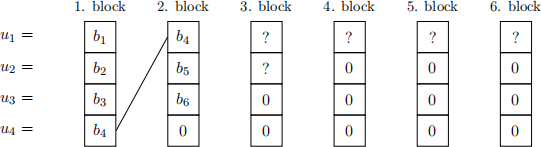
Figure 5: Chaining construction for channels with constant but unknown channel capacity.
