关键词 > C语言代写
HW4
发布时间:2024-06-19
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Assignment
Throughout this homework assignment we consider the following communication system in thecomplex baseband consisting of a transmitter,a time-dispersive AWGN channel, and a receiver,

with the the following system parameters:
• Transmitted symbols: b[n]; symbol duration: T = 2; discrete-time variable at the transmitter n.
• Transmit filter: gT (t) = I[0,T](t)
• Channel filter: gC (t) = a1 δ0 (t — 1) + a2 δ0 (t — 2)
• Receive filter: gR (t) = I[0,Ts] (t)
• Complex-valued zero-mean Gaussian noise process n(t) with power spectral density Sn (f) = N0 .
• Sampling interval at the receiver Ts = T/m; discrete time variable at the receiver k.
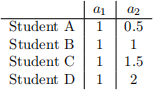
For randomising the solutions, we use the following definitions of Student A-D:
• Student A: You were born in January – March
• Student B: You were born in April – June
• Student C: You were born in July – September
• Student D: You were born in October – December
Problem 1 (5 points)
In this problem, we look at the performance of a receiver that is unaware of the effect of the time-dispersive channel. We consider a binary transmission with BPSK-modulatedequiprobable symbols b[n] ∈ {—1, +1} and assume symbol-spaced sampling at the receiver. That is, m = 1, Ts = T, k = n, and r[k] = r(kTs) with the receive-filter output signal r(t).
a) Sketch the effective impulse response x(t) = gT (t) gC (t) gR (t) and give the resulting discrete-time impulse response f [k] = gC (kTs ). (1 point)
b) Assume that the receiver uses the decision rule (1 point)
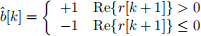
Express r[k + 1] as a function of the data symbols b[n], b[n — 1], . . ., the channel parameters a1 , a2 , and the noise sample w[k + 1].
What limits the performance of this transmission scheme (even in the noise-free case)?
c) For the parameters specified above show that the noise samples w[k +1] in the sampled out- put of the receive filter are uncorrelated and have variance σ 2 = N0 per complex dimension. (1 point)
d) Derive the error probability. (2 points)
Prepare a plot of the error probability over Es /N0 in the range [—20, 30] dB, where we use the energy of the discrete-time impulse response vector f as the received symbol energy, i.e., Es = ⅡfⅡ2 .
Verify the result by analysing the asymptotic cases where the noise variance becomes small (i.e., N0 → 0) and big (i.e., N0 → ∞ ).
Problem 2 (10.5 points)
To improve the performance of the system compared to Problem 1, we now consider the linear equalizer and the decision-feedback equalizer with subsampling with m = 2 (i.e., Ts = T/2) and an observation interval of length L = 3.
a) For the parameters specified above, sketch the effective impulse response x(t) = gT (t) 大 gC (t) 大 gR (t) (note that gR (t) changes with Ts ).
Verify that the noise samples w[k] in the sampled output of the receive filter are uncorrelated and have variance σ 2 = N0 /2 per complex dimension. (1.5 point)
b) Give the discrete-time impulse response f[k] (without leading zeros) and the matrix U of the geometric model for your realization of a1 , a2 (see table above). (1 point)
c) Show for the parameters specified above that the error probability at the output of a linear equalizer c is given as
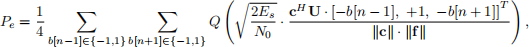
where f is the vector of the discrete-time impulse response f[k] derived in Problem 2(b) and Es = ⅡfⅡ2 . (1 point)
d) Plot the error probabilities for the matched-filter equalizer, the zero-forcing equalizer, and the MMSE equalizer over Es /N0 in the range [0, 15] dB.
Verify your implementation by comparing the asymptotic behaviour of the MMSE equalizer for low SNR and (very) high SNR with the MF equalizer and the ZF equalizer, respectively. (2 points)
e) We consider now the zero-forcing decision-feedback equalizer. Let cFF = [1, 1, 0]T be the chosen zero-forcing feedforward filter.
(i) Find the feedback filter cFB and the decision variable ZDF E for detecting b[n] and give the resulting noise variance for the noise in ZDF E .
(ii) Define the error symbol e[n — 1] = b[n — 1] —b(^)[n — 1]. Express the distribution of e[n — 1], Pr(e[n — 1]), as a function of the average error probability Pe(DFE) .
(iii) Use the following expression for the average error probability to derive a closed-form expression of the average error probability Pe(DFE):
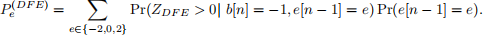
(iv) Plot the error probability over Es /N0 in the range [0, 15] dB, and verify the results by comparing a high-SNR approximation for the DFE with the high-SNR approximation of the linear MMSE equalizer.
(1+1+1.5+1.5 points)
Problem 3 (7 points)
In this last problem, we compare the performance of the above equalization techniques with the performance of a cyclic-prefix OFDM system with N sub-carriers that avoids the equalization problem by transforming the ISI channel into N orthogonal channels. That is, the transmission is organized in blocks of N + L - 1 transmitted symbols b[k],
b = [b[N - (L - 1)], . . . , b[N - 1], b[0], . . . , b[N - 1]],
where the first L - 1 symbols are the cyclic prefix, and the remaining N symbols are the samples of the BPSK-modulated data symbols B[l] ∈ {-1, +1}, modulated by the sub-carriers,
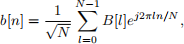
![]() where the factor √N is chosen to normalize the sub-carriers to unit energy to ensure a fair comparison with results from Problem 1 and 2, and l is the discrete frequency variable of the DFT.
where the factor √N is chosen to normalize the sub-carriers to unit energy to ensure a fair comparison with results from Problem 1 and 2, and l is the discrete frequency variable of the DFT.
The receiver uses the receive filter gRX (t) as specified above with symbol-spaced sampling (i.e., m = 1, Ts = T, and n = k, as in Problem 1), extracts the last N samples of the block of received samples r[k] to remove the cyclic prefix, and employs the DFT for demodulating the subcarriers:
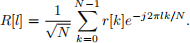
(Note that the time variable at the receiver k = n for m = 1.)
a) Give the sampled impulse response h[k] (remove leading zeros due to transmission delays) and the cyclic-prefixlength. (1 point)
b) For the resulting N parallel sub-carrier channels
derive an expression for the fading coefficients H[l] and their amplitudes |H[l]|, and give the noise variance of the resulting Gaussian noise samples after OFDM demodulation, W [l]. (2 point)
c) Assume that the receiver employs phase compensation in order to be able to employ a sign-based decision rule for coherent detection,
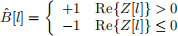
![]() with the decision variable Z[l] = √N |H[l]|B[l] + W, [l], where complex W, [l] are the noise samples after phase rotation.
with the decision variable Z[l] = √N |H[l]|B[l] + W, [l], where complex W, [l] are the noise samples after phase rotation.
Derive an expression for the average error probability, averaged over the N sub-carriers, and a high-SNR approximation. (1.5 point)
d) For N = 16, Es = Ⅱ[h]Ⅱ2 (i.e., the energy of the sampled impulse response h[k]), plot the exact error probability and the high-SNR approximation over Es /N0 in the range [0, 15] dB. (1 point)
e) Comment on how the results in Problem 1-3 reflect the expected behaviour. If there are deviation from the expected behaviour, try to give reasons.
Make a suggestion on how the performance of the OFDM system can be approved. (1.5 point)

