关键词 > LineareAlgebra
Lineare Algebra II 2024
发布时间:2024-06-19
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Lineare Algebra II
Aufgabe 1. Beschreiben Sie alle abelschen Gruppen der Ordnung 1176 bis auf Isomorphie.
Aufgabe 2. Seien G und H abelsche Gruppen und φ : G → H ein Homomorphismus. F¨ur m ∈ Z bezeichne µm(G) : G → G, g }→ mg und µm(H) : H → H , h }→ mh die Homomorphismen gegeben durch Multiplikation mit m.
a) Zeigen Sie, dass das Diagramm
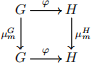
kommutiert, d.h., zeigen Sie φ ◦ µm(G) = µm(H) ◦ φ .
b) Zeigen Sie, dass sich φ zu einem Homomorphismus
φ| ker(µm(G)): ker(µm(G)) → ker(µm(H))
einschr¨anken l¨asst.
c) Zeigen Sie: Falls φ ein Isomorphismus ist, dann ist auch φ| ker(µm(G)) ein Isomorphismus.
Aufgabe 3. Sei n ∈ N>0 . Wir fassen die Elementeder zyklischen Gruppe (Z/n, +) als Restklassen modulo n auf, und schreiben [m] f¨ur die Restklasse von m ∈ Z. Zeigen Sie: Ein Element [m] ∈ Z/n ist ein Erzeuger von (Z/n, +) genau dann, wenn m und n teilerfremd sind.
Aufgabe 4. Sei n ∈ N>0 und A ∈ Cn×n.
a) Zeigen Sie, dass es Matrizen Anil ∈ Cn×n und Adiag ∈ Cn×n gibt, sodass
(i) A = Anil+ Adiag
(ii) Anil ist nilpotent, d.h., es gibt ein N ∈ N sodass Ani(N)l = 0.
(iii) Adiag ist diagonalisierbar
(iv) AnilAdiag = AdiagAnil.
[Hinweis: Betrachten Sie die Jordan-Normalform von A.]
b) F¨ur B ∈ Cn×n und λ ∈ C definieren wir
Vλ(B) = {v ∈ Cn | ∃k ∈ N : (B − λEn)k (v) = 0} .
Dann ist Vλ(B) ⊂ Cn genau jener Untervektorraum, auf welchen eingeschr¨ankt B eine Jordan-Normalform mit auschließlich Jordan-K¨astchen zum Eigenwert λ hat. Insbesondere ist Vλ(B) = {0} f¨ur alle bis auf endlich viele λ ∈ C, und außerdem

Falls B diagonalisierbar ist, dann ist Vλ(B) = Eig(B,λ).
Sei A = Anil + Adiag eine Zerlegung, welche die vier Eigenschaften aus a) erf¨ullt (nicht notwendigerweise jene Zerlegung, die Sie konstruiert haben). Sei v ∈ Vλ(Adiag). Zeigen Sie:
(i) F¨ur alle k ∈ N gilt (A − λEn)k (v) = An(k)il (v).
(ii) Es gilt v ∈ Vλ(A), und folglich Vλ(Adiag) ⊂ Vλ(A).
[Hinweis zu (i): Schreiben Sie A = Anil + Adiag und verwenden Sie die binomische Formel (x + y) k = P ki =0xi y k−i. Was m¨(u)ssen Sie beachten, wenn Sie diese Formel benutzen?]
c) Zeigen Sie, dass Vλ(Adiag) = Vλ(A) f¨uralle λ ∈ C. [Hinweis: In b) wurde bereits die Inklusion
Vλ(Adiag) ⊂ Vλ(A) gezeigt. F¨ur Gleichheit benutzen Sie (1)].
d) Sei A = Anil(′) + A′diag eineweitere Zerlegung, welche (i)-(iv) aus Teilaufgabe a) erf¨ullt. Zeigen
Sie, dass
Adiag = A′diag .
Folgern Sie, dass die Zerlegung von A in eine nilpotente und eine diagonalisierbare Matrix eindeutigist,d.h., es gilt auch Anil = Anil(′) . Diese Zerlegung heißt Jordan-Chevalley-Zerlegung.
[Hinweis: Zeigen Sie zuerst, dass Vλ(Adiag) = Vλ(A′diag) f¨ur alle λ ∈ C.]

