MATH2014 Algorithms SEMESTER 2 EXAMINATION 2021/22

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH2014 Algorithms

SEMESTER 2 EXAMINATION 2021/22

1. (a) Compute a minimum cost spanning tree using the Jarnik-Prim-Dijkstra algorithm on the following graph:

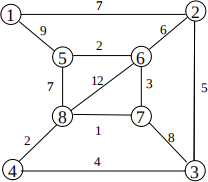
(b) Consider now the problem of, given an undirected graph G = (V, E) with a cost function c : E → Z + \ {0}, finding a spanning tree minimizing the product of the costs of the edges it contains. Explain how to solve this problem using one of the algorithms presented in the module.             [10 marks]

2. Consider the following weighted undirected bipartite graph G = (V, E).

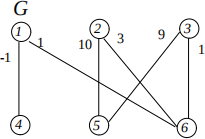
(a) Find a maximum-weight matching in the graph using the algorithm seen in the lectures. Report, for each iteration of the algorithm, a copy of the graph G (in which the current matching is highlighted) and the corresponding auxiliary graph G' (in which the augmenting path you have found is highlighted).                    [10 marks]

(b) State and justify the complexity of the algorithm you used.            [10 marks]

3. Consider the problem of finding a maximum flow from node 1 to node 6 in the following directed graph G = (V, A). The two numbers on each arc are, respectively, the flow currently on that arc and the arc capacity.

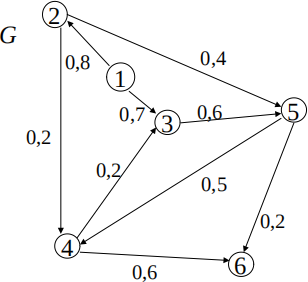
(a) Solve the problem via the Ford-Fulkerson algorithm, starting from the given flow shown in the figure. Report, for each iteration of the algorithm, both the graph G (updated with the flow at that iteration) and the corresponding auxiliary graph G'(with the corresponding residual capacities). On the latter, also indicate the augmenting path you have found.

After that, deduce from the solution you have found a 1–6 cut of minimum capacity in G. Highlight the set S* ⊂ V that induces it and the arcs the cut contains. Calculate the cut capacity.           [10 marks]

(b) Show that the Ford-Fulkerson algorithm, in the version studied in the module, does not enjoy a polynomial complexity. You may use an example, if you wish.            [10 marks]

4. Consider the following undirected graph.

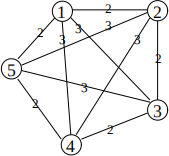
(a) Find a (not necessarily optimal) solution to the Metric Undirected Traveling Salesman Problem (MUTSP) on it by applying the 2-approximate algorithm seen in the lectures. Draw the solution you have found and report its cost.        [10 marks]

(b) Show that the algorithm you applied yields a 2-approximate solution.               [10 marks]

5. (a) Solve the following instance of the boolean SATisfiability problem (SAT) with the partial enumeration algorithm:

(Y1 ∨ Y2 ∨ Y3) ∧ (Y1 ∨ −Y2) ∧ (−Y1 ∨ −Y3) ∧ (−Y1 ∨ Y3) ∧ (Y4 ∨ −Y1)

[10 marks]

(b) Does the algorithm you applied run in polynomial time? Explain your answer.                    [10 marks]