MATH226 Problem Sheet 8

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH226 Problem Sheet 8

Throughout the following problems,

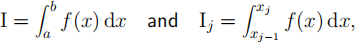
for a function f and real numbers a and b with xj = a+j∆x and ∆x = (b−a)/N. The subinterval midpoint is given by x*j = (xj−1 + xj )/2.

8.1 (a) Write a Maple procedure that approximates I using the area of a rect-angle for each subinterval. The procedure should take as its arguments a function f, real numbers a and b, a number of subintervals N and a parameter t ∈ [−1, 1]. The height of the rectangle for subinterval j should be f(x*j + t∆x/2), so that t = 1 corresponds to using the upper right corner, t = −1 the upper left, etc.

(b) (i) Choose some integrals and experiment with your procedure to find out which value for t gives the lowest error. Make sure you set the number of subintervals so that ∆x < 1 and avoid division by zero, etc. You should find that (approximately) the same value for t works best in all cases. Consider a sufficient number of examples to convince yourself that this result does not occur by chance.

(ii) Can you think of a way to explain why this happens?

Hint: consider the case in which f(x) is a linear function (i.e. f(x) = mx + c).

8.2 Let h = (a + b)/2. The coefficients wj in the approximation

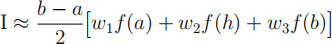
are chosen so that f(x) = x 2 is integrated exactly for arbitrary end points a and b. By writing both sides in terms of a and b and matching coefficients, find the values of w1, w2 and w3.

8.3 (a) (i) Calculate the exact value of Ij for the case where f(x) = x3. Express the result in terms of ∆x and x*j, and simplify as far as possible; your answer should not involve xj or xj−1.

(ii) Apply Simpson’s rule to approximate Ij , again for the case where f(x) = x3. Write your answer in terms of x*j and ∆x and simplify as far as possible.

(b) In view of your answers to part (a), what can be said about the error that occurs if Simpson’s rule is used to approximate Ij for the arbitrary cubic equation

f(x) = c3x 3 + c2x 2 + c1x + c0,

where c3, . . . , c0 are constants? Justify your answer.

8.4 (a) Use the formulae in §5.4 to obtain the weights for the four point Newton–Cotes quadrature rule for [−1, 1].

Make sure your nodes really are equally spaced!

(b) Write down the four point Newton–Cotes rule for the arbitrary interval [xj−1, xj ].

(c) Determine the leading order error in the four point Newton–Cotes rule.

(d) Does the four point rule offer a significant improvement in accuracy over Simpson’s rule? Explain your answer.

8.5 Throughout this problem, Digits should be set to at least 16 in Maple.

(a) Write a Maple procedure that implements the four point Newton–Cotes rule. The procedure should take as its arguments a function f, lower and upper bounds a and b and the number of subintervals N. It should return the approximate value of the integral I as its result. Ensure your procedure does not evaluate the integrand more than once at any point.

(b) Choose a function f (not a polynomial; avoid division by zero, etc.) and an interval [a, b]. Use your four point quadrature procedure to estimate the value of I using 10, 20 and 50 subintervals, and calculate the relative error in these estimates.

You can obtain an accurate value for the integral using the command

evalf[32]( Int( f( x ) , x = a .. b ) )

(c) Repeat the calculations from part (b) using Simpson’s rule in place of your four point procedure. Compare the errors in the estimates from Simpson’s rule and the corresponding estimates from four point rule using the same number of subintervals. Do the results agree with your predictions from problem 8.4?

(d) The comparison used in part (c) isn’t ‘fair’, in the sense that Simpson’s rule with N subintervals requires 2N + 1 values for the integrand, whereas the four point rule requires 3N + 1 values. With this in mind, repeat the calculations from part (c), using 15, 30 and 75 subintervals. Compare your new results to those obtained in part (b). Which rule performs better?

(e) What is the approximate ratio of the error in Simpson’s rule using N = 75 and the error in the four point rule using N = 50? Why does this happen?