37007 Probability Theory and Stochastic Analysis Sample Exam Autumn 2024

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

37007 Probability Theory and Stochastic Analysis

Sample Exam Autumn 2024

Assume all RVsand SPs are adapted to suitable (filtered) probability spaces.

Question 1.

Consider the joint-Gaussian process

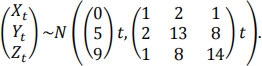
(a) Find the distribution of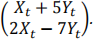

(b) Find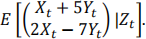

(c) Let Bt, t  ≥ 0, be a standard Brownian motion and set

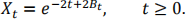
Find Pearson’scorrelation corr(xt, xs ) where 0 ≤ s < t.

(d) Let Bt, t ≥ 0, be a standard Brownian motion, x  ∈ ℝ and set

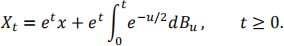
Determine if xt  is a Markov process.

Question 2.

Consider the Poisson process Nt, t  ≥ 0 , with intensity λ  =  1.

(a) Calculate

P(N1  = 4, N3  = 5|N5  = 7).

Now define the compound Poisson

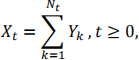
with Nt  as above and where Yk, k  ∈ {1,2, … , Nt }, has the distribution

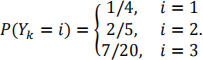
Assume that Nt  and the Yk  are all independent from each other.

(b) Find E[eiuxt].

(c) Let Bt, t  ≥ 0, be a standard Brownian, m, r  ∈ ℝ and σ  > 0 and consider the process

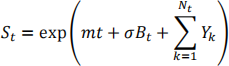
adapted to the filtered probability space (Ω, ℱ, Q, (ℱt )t≥0). Find m such that

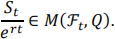
Question 3.

Consider the homogenous, discrete-time Markov chain xt, t  = 0, 1,2 …, taking states xt   ∈ {x1  = 8, x2  = −4, x3  = −6} with one-step transition matrix and initial distribution

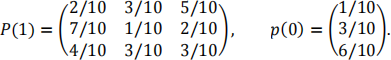
(a) Calculate E[x3 |x1  = −4].

(b) Using the criteria of Theorem 5 on page 28 of Chapter 5 notes, determine if xt is ergodic.

Now consider the homogenous, continuous-time Markov chain Yt, t  ≥ 0, taking states Yt  ∈ {1,2,3} with transition matrix (when jump occurs)

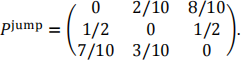
Assume that the expected values of weighting times for jumps from states 1, 2 and 3 are 1/2, 1/6 and 1/7 respectively.

Consider the process

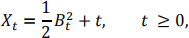
where Bt, t   ≥ 0, is astandard BM.

(a) Using Definition 1 page 6 Chapter 11 Notes, derive the drift function for xt. (b) Find the Ito representation of xt.

Now let

yt  = ext,   t ≥ 0.

(c) Find the Ito representation of yt.

(d) Write down the Kolmogorov forward equation for

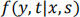
where

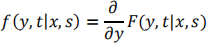
with

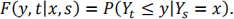
Question 5.

(a) Let Bt, t ≥ 0, be a standard Brownian motion and consider the process

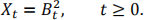
Determine if xt  is a martingale, submartingale or supermartingale.

(b) Let ξt, t ∈ {0, 1, … }, be a sequence of independent RVs and set

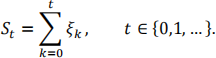
Find the Doob-Meyer decomposition of exp(st ).

(c) Let Bt, t ≥ 0, be a standard Brownian motion on (Ω, ℱ, P) and define

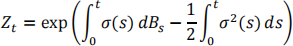
where σ(t) > 0 is anon-random function of time such that

Determine the distribution of

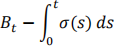
on the probability space (Ω, ℱ, Q) defined by

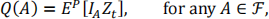
with IA  the indicator of event A.