Phys 139: Problem set 6

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Phys 139: Problem set 6

Due by 11:59pm on Monday, May 20

May 14, 2024

1. Calculate the Reynold’s number for blood flow in the human aorta, and in a capillary.

2. Consider a cylindrical pipe of length L and radius R, with L >> R. An incompressible fluid of viscosity η fills the pipe, and a pressure difference ∆p is applied across the length of the pipe to cause the fluid to flow with a velocity field ~v(z, r, θ), given a cylindrical coordinate system in which the pipe is oriented in the z direction, there is a radial distance r from the center of the pipe, and an azimuthal angle θ. The flow at the surface of the pipe can be taken to be zero, v(r = R) = 0.

(a) First, do a simple dimensional analysis calculation to predict the dependence of the flow rate on the various parameters– particu-larly, predict the rough magnitude of the fluid velocity, |v|, con-sidering whether it should increase or decrease with η, ∆p, L, and the cross sectional area A ∼ R2 .

(b) Now we calculate the actual flow field. Assume low-Reynolds number flow. Show that the flow obeys the following equation:

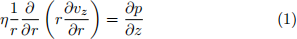
(c) In the above equation, the left side depends only on r and the right on z, so both must equal a constant, independent of r and z. Use this, and the boundary conditions, to find the velocity field. How does the maximum velocity compare to your scaling prediction?

(d) In deriving the Navier Stokes equation, we noted that a volume element of fluid, dxdydz, in a velocity gradient dvy/dx, will feel a shear force ~F = ηdydz(dvy/dx)ˆy on its top surface. One can thus define a shear stress as the shear force per unit area, σy ≡ Fy/(dydz) = η(dvy/dx). Calculate the numerical magnitude of the shear stress near the wall of a blood vessel, for various types of fluid flow (say, for the capillary and aorta). Leukocytes are white blood cells of roughly 10 µm diameter that, in searching for infection to battle, will stick to the wall of the blood vessel, and roll along the wall. Estimate the force (in picoNewtons) on a leukocyte from the shear stress (i.e. given F ∼ σA, where A is the cell area); this sets a scale for the bond strengths that hold the leukocyte onto the blood vessel wall.

3. Chlamydomonas reinhardtii is a ≈ 10 µm cell that swims at a speed of around 60 µm/s. Calculate the Reynold’s number of motility. View videos of this organism swimming (such as here or here), and discuss the relevance of the Scallop theorem to the organism’s swimming mo-tion.

4. Here, the goal is to derive the Berg Purcell sensing limit by an alternate means to that done in class. Consider a receptor patch of length scale a on the surface of a bacterium that is immersed in a chemoattractant of bulk concentration c. Use a diffusion-to-capture model to estimate the flux, J, of chemoattractants onto the receptor. Assuming the bacterium senses for a time τ , calculate the normalized fluctuations, ¯σ = στ /h N(τ )i , where στ is the standard deviation in the number of molecules sensed in time τ , and h N(τ )i is the mean number sensed in that time. Comment on your answer.

5. Dictyostelium discoideum, or ‘Dicty’, is an amoeba, commonly termed a ‘slime mold’, in which individual cells, in certain conditions, emit chemoattractants (notably cyclic AMP, cAMP) that guide other cells towards them in order to assemble (Voltron-like) into a larger multi-cellular entity. Individual cells are about 10 µm long, and it appears that the amoeba orients its motion using direct spatial sensing, i.e. comparing chemoattractant concentrations as sensed by receptors lo-cated on opposite sides of the cell.

(a) Explain how this ‘direct sensing’ is different than the mechanism used by swimming bacteria.

(b) An experiment is done in which a micropipette with a 10 µm radius is filled with cAMP at 10−4 M concentration, and placed near a colony of Dicty. You can see a video of this sort of experi-ment here. Calculate the farthest distance at which an individual Dicty cell will be able to reliably detect, and orient itself to, the cAMP concentration gradient. Do this by writing down 1) the sensing noise limit in terms of the concentration field, c(r), and

2) the signal, δc/c, which you can also find from c(r). Make a single plot that contains both curves (i.e. signal vs radius and noise vs radius), and give an interpretation to all regimes of this plot. Note: While these creatures actually crawl along surfaces, the chemoattractant diffuses in three dimensions, so use a 3-D geometry to calculate the shape of the concentration field, c(r). Assume the cell averages signals for a time period τ ≈ 3 s.