关键词 > ECON0060
ECON0060: ADVANCED MICROECONOMETRICS SUMMER TERM 2020
发布时间：2024-06-04
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
SUMMER TERM 2020
ECON0060: ADVANCED MICROECONOMETRICS
PART A
Answer all questions. 50 marks total.
Question 1 (25 marks total)
Suppose you have data on yit and xit for i = 1,...,N and t = 1,...,T. Both yit and xit are scalars. Consider the model
yit = ⇢yit-1 + βxit + αi + vit , (1)
vit = uit + φui,t-1 ,
where (⇢ , β , φ) are parameters, αi is an unobserved individual efect, and uit is an unobserved shock that is iid across i and t for all i = 1,...,N and t = 0,...,T. The correlation between αi and xit is not necessarily 0. Make the following weak exogeneity assumption:
E(uit |xi1,...,xit ) = 0 8t = 1,...,T.
a. Under these assumptions, OLS applied to model (1) does not yield consistent parameter estimates. Give as many reasons as you can to justify this statement.
b. Eliminate the fixed efect from the model by first diferencing to obtain:
△yit ⌘ yit − yit-1 = ⇢△yit-1 + β (xit − xit-1 )+ vit − vit-1 .
Does OLS applied to this equation provide consistent estimates of (⇢ , β)? Explain.
c. How can you estimate (⇢ , β , φ) consistently?
d. What condition is required on xit?
Question 2 (25 marks total)
Consider the static panel data model
yit = βxit + εit ,
where i = 1, . . . ,n denotes individuals, and t = 1, 2 denotes time. The single regressor xit and the error term εit are distributed as follows
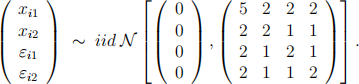
For any real number q define the diferences △ (q)yi = yi1 − q yi2 , △ (q) xi = xi1 − qxi2, and △ (q) εi = εi1 − q εi2 . For q = 1 these are standard first diferences. The OLS estimator of the regression of △ (q)yi on △ (q) xi is given by
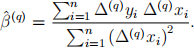
a. Is the OLS estimator of the regression of yit on xit consistent for β? Explain.
b. Show that there exist a constant c such that
xi1 = cαi + ˜(x)i1, xi2 = αi + ˜(x)i2 , εi1 = αi + ui1 , εi2 = αi + ui2 ,
where αi ,˜(x)i1 ,˜(x)i2 , ui1 and ui2 are mutually independent standard normal random variables. What is the value of c? (Hint: you can start with the representation of xi1 , xi2 , εi1 and εi2 given here. Then show that xi1 , xi2 , εi1 and εi2 are jointly normal with mean zero, and that there exists c that delivers the 4 × 4 variance-covariance matrix above).
c. For q = 1, explain briefly whyβ(ˆ)(1) is consistent and asymptotically normal, and derive the asymptotic variance ofβ(ˆ)(1) . (Hint: use the result of part b.)
d. Show that there exists a value q 
1 for whichβ(ˆ)(q) is also a consistent estimator for β . For this value of q explain briefly whyβ(ˆ)(q) is consistent and asymptotically normal, and derive the asymptotic variance ofβ(ˆ)(q) . (Hint: use the result of part b.)
e. Would you recommend to use β(ˆ)(1) or the estimatorβ(ˆ)(q) from part d.?
PART B
Answer all questions. 50 marks total.
Question 3 (25 marks total)
Consider the following Type II Tobit selection model:
y
1 = xi1β1 + εi1
yi1 = yi2 · y
1
yi2 = 1[xi2β2 + εi2 ≥ 0]
from which one obtains a random sample of observations denoted {(y1i)y2i)x1i)儿2i) : i = 1)...)n}. The variables xi1 and xi2 are vectors of dimension k1 and k2 respectively. y
1 is the outcome of interest but is only observed when yi2 = 1. Assume that (εi1) εi2) and 儿i = (儿i1)儿i2) are independent and that (εi1) εi2) are bivariate normally distributed, each with mean zero and with uar (εi1) = σ11 , uar (εi2) = 1, and cou (εi1) εi2) = σ12 .
a. What is the selection probability Pr(yi2 = 1|儿i ) in this model? Which parameters can be estimated using the selection probability alone? How can you consistently estimate the parameters of the selection probability? State any additional conditions required.
b. What is E(yi1|yi2 = 1, xi )?
Hint: Since εi1 and εi2 are jointly normal, εi1| εi2 ~ N (σ12εi2 ) σ11 - σ 1(2)2 ). Further, recall that since εi2 is a standard normal random variable, for any real number c,
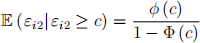
where φ (·) and Φ (·) denote the standard normal pdf and cdf, respectively.
c. Solve for the conditional density for yi1 given yi2 = 1 and x. What is the log likelihood for this model?
Hint: Since εi1 and εi2 are jointly normal, the conditional density of εi1 given εi2 ≥ c is
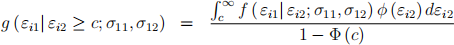
where f (εi1|εi2; σ11) σ12 ) is the density of εi1 conditional on εi2 . You can use this expression in your answer.
d. Propose two diferent ways to consistently estimate β1 . Which provides a more efficient estimator asymptotically?
e. Why might one wish to test the hypothesis that σ12 = 0? What implication would this have?
Question 4 (25 marks total)
Let y1i ∈ {C,B, A} be the credit rating for consumer i where C < B < A. That is, C is the
lowest rating and A is the highest. Suppose a consumer’s credit rating, y1i, is determined by y 1(*)i ,
an unobserved measure of “credit worthiness”, according to the following ordered probit model
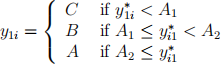
where (A1 , A2 , A3 ) are unknown cutofs to be estimated. Further, assume that
y 1(*)i = x1iβ1 + y2i√ + ε 1i
y2i = x2iβ2 + v2i
where y2i is credit card spending in the past year and (x1i, x2i) are observable demographic variables that afect credit worthiness and credit card spending. The variables (ε 1i, v2i) are unobservables. Assume that v2i ~ N (0, eαx2i). In other words, v2i is heteroscedastic with
variance that depends on x2i. Define the homoscedastic error ε2i = e- α2(x)2i v2i and assume that
(ε 1i, ε2i) are jointly normally distributed independent of (x1i, x2i). In particular, assume that var(ε 1i) = var(ε2i) = 1 and cov(ε 1i,ε2i) = P. You observe a random sample with N observations on (y1i, y2i, x1i, x2i).
a. Propose √N consistent estimators for (β2, α).
b. Show that ε 1i = Pε2i + η 1i where η 1i is normally distributed independent of (x1i, x2i, ε2i). What is the variance of η1i?
c. Propose a two-step method for consistently estimating (β1, √ , A1 , A2, P).
d. How would you estimate the average partial efect of (x1i, y2i) on credit ratings?
