comp2022/2922 Assignment 4 – Automata

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

comp2022/2922

Assignment 4 – Automata

s2 2021

Problem 1.    (8 marks)

1. Consider the NFA over the alphabet {a, b} with initial state q1, final states {q2, q5}, and transition relation:

(a) provide an equivalent DFA.

(b) provide a short English description of its language.

2. Consider the DFA over the alphabet {a, b} with initial state q1, final states {q4, q5}, and transition function:

(a) provide an equivalent RE.

(b) provide a short English description of its language.

Problem 2.    (6 marks) Consider the language L of strings u over alphabet {a, b} such that the number of times b occurs in u is divisible by the number of times a occurs in u. For example, bab, bba, bababb, bbbbbbbbaa, aaa are all in the language, but aba, bbbaaaa, bb, babaaa are not. Prove that L is not regular using the fooling argument. Format your proof as in lectures.

Problem 3.    (6 marks) Provide an NFA that decides whether a given proposi-tional logic formula in CNF over three atoms is satisfiable.

The input formula will be given in the following format: Each clause is a string over the alphabet x, y, z, X,Y, Z. Here x, y, z represent atoms and X,Y, Z repre-sent their negations. The clause is the disjunction of these literals. Clauses are separated by #. The formula is the conjunction of the clauses.

For instance, the formula (x ∨ y) ∧ (¬z ∨ y) ∧ ¬x is represented by the string xy#Zy#X. Since the formula is satisfiable, the NFA should accept the string. On the other hand the formula (¬x ∨ y ∨ ¬z) ∧ (¬y ∨ ¬z) ∧ z ∧ x is represented by the string XyZ#YZ#z#x. Since the formula is not satisfiable, the NFA should reject this string.

Problem 4.    (5 marks)

Consider the following Turing machine over input alphabet {0, 1, 2, 3, a}, state set {q1, q2, qaccept, qreject}, initial state q1, and transition function:

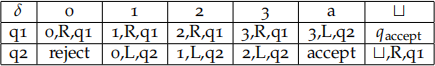
(a) Provide a DFA that recognises the language recognised by the TM.

(b) Provide a short English description of the language.

Problem 5.    (9 marks)

Let Σ = {0, 1, #}. For each of the following languages, build deterministic one-tape TMs that recognise the language and that halt on every input:

1. (3 marks) The language consisting of strings u#v for u, v ∈ {0, 1}^∗  such that |u| < |v|. For instance 111#0000 should be accepted and 101#011 should not.

2. (3 marks) The language consisting of strings u#v for u, v ∈ {0, 1}^∗ such that either (i) |u| < |v|, or (ii) |u| = |v|, u ≠ v, and if i is the left-most position where u differs from v then ui = 0 and vi = 1. For instance, 111#0000 and 0010#0101 should be accepted, but 100#1 and 010#001 should not.

3. (3 marks) The language consisting of non-empty strings x ∈ {0, 1, #}⁺ such that if x = uwwv for some u, v, w ∈ {0, 1, #}^∗ then w = . In other words, x does not have a non-empty substring of the form ww. For instance, the following strings should be accepted: 01# and 1#0#10 and 0#01, while the following strings should not: 01#0101# and 001.

You can assume the input to the TM is always well-formed. That is, for the first two problems all inputs will be of the form u#v for u, v ∈ {0, 1}^∗, and in the third problem all inputs will be of the form x ∈ {0, 1, #}⁺.

Problem 6.    (6 marks)

Unfortunately, CliqueFinder went bankrupt when it was discovered that the prob-lem they were trying to solve was NP-hard. Fortunately, you were able to get a new job at PathFinder, a company that solves the more managable problem of determining whether there is a path between two nodes (it also publishes RPGs, but that’s a story for another time).

Your task is to determine, given a directed graph (with no self-loops) represented as an adjacency matrix, whether there is a path from the first node and the last node. You’ve had enough of propositional logic, so you decide to solve this problem using a Turing machine.

Input will be given to you over the alphabet {0, 1,s, #}. The graph contains n nodes, n ≥ 2. The i-th node is represented by a string of length n, whose jth letter is s if i = j (representing the special case of no self-loop), and otherwise a 1 if there is an edge from node i to node j, and a 0 if there is no edge from node i to node j. Nodes are separated by # characters. You may assume that the input is well-formatted.

For example, the graph with nodes {1, 2, 3, 4} and edges {(1, 2),(2, 3),(3, 1),(2, 4)} is represented by the input string:

s100#0s11#10s0#000s

Moreover, since there is a path from the first node 1 to the last node 4, for instance the path (1, 2, 4), your Turing Machine should accept that input string.

The following input represents the same graph with edge (2, 4) removed, and since there is no longer a path from the first node to the last node, your Turing Machine should reject the input string

s100#0s10#10s0#000s

Marks will be awarded based on the proportion of test cases passed. For full marks, you should aim to solve any instance with n ≤ 10 in under 10⁶  steps. Note that your machine should work for general n and always (eventually) out-put the correct answer for any well-formatted input. You should not make any assumptions about the size of n, or about the distribution of edges.