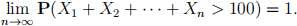STAT 463/853 – Fall 2021 Midterm test 1

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

STAT 463/853 – Fall 2021

Midterm test 1

1. (Distribution of random variables) Let 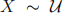[0, 3] have uniform distri-bution on the interval [0, 3]. What is the probability that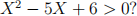 

2. (PDF and CDF) a) Consider the following family of probability densities

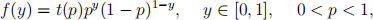
defined on the interval [0, 1] and depending on the parameter p ∈ (0, 1). Here t(p) is a normalizing coefficient. Determine the value of this coefficient.

b) (For students of the class STAT-853 only) Determine the cumulative distribution function F(y) corresponding to the probability density (1).

3. (Expectation) A box contains n tickets, numbered 1, 2, ..., n. A ticket is drawn at random from the box, its number is registered, and the ticket is returned to the box. Another ticket is drawn at random from the box, again its number is registered, and the ticket is returned to the box. This procedure is repeated until first such moment T when all n numbers have been registered. Obviously, the moment T can be represented as the following sum

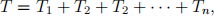
where T1 = 1 is waiting time till the first “new” number is obtained; T2 is the waiting time till another “new” number is obtained, i.e., a number different from the previous one; T3 is the waiting time till yet another “new” number is obtained, different from the previous two; etc.

a) What is the distribution of i) T2 ? ii) T3 ? iii) Tn ?

b) Find the expected value E T.

4. (Moment generating function) The moment generating function (MGF) of a random variable X is given by

Suppose X is a gamma random variable whose pdf is given by

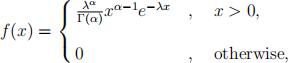
for some α > 0 and λ > 0.

a) Calculate the MGF MX(t).

b) For which t is MX(t) finite?

5. (Poisson, exponential, and geometric distributions) Suppose X has exponential distribution 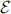(λ). Denote 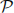(λ) the Poisson distribution with parameter λ > 0. Let Y be a random variable whose conditional distribution given X = x is 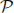(x). Thus, the joint distribution of X, Y is of the mixed type.

a) Determine the marginal distribution of Y. Hint: Recall the gamma integral,

b) Show that the random variable Y + 1 has a geometric distribution.

6. (LLN) Let X1, X2... be a sequence of independent, identically distributed random variables having finite second moment and positive expected value µ > 0. Prove that