COMP2300/COMP6300 Applied Cryptography

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

COMP2300/COMP6300 Applied Cryptography

Assignment 2

Objectives

This assignment has been designed to test your knowledge of public-key cryptography and application of cryptography in cryptocurrencies.

Notes

● Assumptions (if any) must be stated clearly in your answers.

● There may not be one right answer for some of the questions. So, your explanations need to present your case clearly. The explanations you provide do not have to be long; conciseness is preferred to meandering.

● The hints to solutions of almost all questions in this assignment are in the lecture slides, and the textbooks [Sma16] and [NBF+16].

Submission

● On line submission via Turnitin.

Assignments will be marked and returned online. There are no hardcopy submissions for written assignments.

Ensure you submit the correct file. The submission process shows you a complete preview of your entire assignment after you have uploaded it but before you have submitted it. Carefully check through every single page to ensure everything is there and the correct version has been uploaded.

Multiple submissions may be possible via Turnitin prior to the final due date and time of an assessment task and originality reports may be made available to students to view and check their levels of similarity prior to making a final submission. Students are encouraged to use these reports to ensure that they do not breach the Academic Honesty Policy through high levels of similarity (plagiarism).

Teaching staff will use the report to judge whether plagiarism has occurred and whether penalties should apply for breaches of the Academic Honesty Policy. Any similar text identified by Turnitin will be considered carefully to see if it is indeed a breach of the Academic Honesty Policy.

Question 1 (8 marks)

This question tests your knowledge of what constitutes a group. Let n be a composite number. Let X = {1, 2, . . . , n − 1}.

(a) Let x ∈ X. Show that if there are integers a, b such that ax + bn = 1, then gcd(x, n) = 1. (2 marks)

(b) Let x ∈ X. Show that if gcd(x, n)  1 then ax ≡ 1 (mod n) has no solution for any integer a. (2 marks)

(c) Show that there is at least one element x ∈ X, such that gcd(x, n)  1. (2 marks)

(d) Let ∗ be multiplication modulo n. That is, for x, y ∈ X, x ∗ y = xy (mod n). Prove that (X, ∗) is not a group. (2 marks)

Question 2 (4 marks)

An encryption system is considered malleable if given a ciphertext of some unknown plaintext, it is possible to obtain a valid ciphertext of a related plaintext without even knowing the contents of the plaintext. This is problematic depending on the application. For instance, in bidding for a contract, a company might outbid its competitor by simply multiplying it’s rival company’s encrypted bid by 0.9, without even knowing the bid [DDN03]. The following questions relates to the malleability of the Elgamal cryptosystem taught in the lecture.

(a) Suppose we are given the ciphertext c = (c1, c2) of some unknown message m, where c1 ≡ g^k (mod p) for some unknown random integer k ∈ Zp−1 and c2 ≡ m · h^k  (mod p), where h is the public key of some unknown private key x, in the Elgamal cryptosystem. Let m0 be a message that you know. Can you obtain a valid ciphertext of the message m · m' without knowing m? (2 marks)

(b) Let p = 739. Given the following ciphertext of some message m1 encrypted using randomized Elgamal, what is the ciphertext of m1 · m2, where m2 ≡ 2 (mod p)? Show the steps in PARI/GP. (1 mark)

(c1, c2) = (246, 609)

Note that the integers are reduced modulo p.

(c) Continuing from part(c), suppose the private key is x = 419. What is the message m1? (1 mark)

Question 3 (6 marks)

Let X be a random variable taking on n values with probabilities p1, p2, . . . , pn. We will assume all proba-bilities are non-zero. Recall from Lecture 9 that the min-entropy of X, denoted E∞(X), is given by

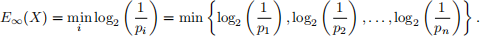
We will drop the logarithm and simply work with the quantity:

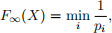
by noting that whatever pi minimizes F∞(X), also minimizes E∞(X). Also, note that if X is uniformly distributed then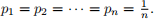

(a) Show that if X is not uniformly distributed then necessarily one of the pi’s is > 1/n. (2 marks)

(b) Show that if X is not uniformly distributed then F∞(X) < n. (2 marks)

(c) Argue that min-entropy is the highest if X is uniformly distributed. What is the min-entropy (E∞(X)) in this case (2 marks)

Question 4 (2 marks)

Recall from Lecture 10 that a 51% attacker is an attacker who holds at least 51% of the total hash power. Let α represent the proportion of hash power held by this attacker. Then, α ≥ 0.51. Suppose this attacker wants to suppress Carol’s transactions by not including any of her transactions. To do so, whenever the attacker (or the attacker’s nodes) solves the hash puzzle, it proposes a block without Carol’s transactions. Show that the attacker will be successful in the sense that the longest valid consensus chain will eventually be the one proposed by the attacker. Why this will not be the case if α < 0.5? (2 marks)

Question 5 (10 marks)

Recall hash puzzles from Lecture 10. In this question, we will see how they work in practice. This question requires programming in a language that has an implementation of SHA-256 hash function. You could use Java to program, although, you are free to use any other language with a library containing SHA-256, e.g., Python’s hashlib (which maybe easier to implement). Create an integer s containing all the digits in your student ID. For example, if my student ID is MQ12345678, then s = 12345678. Let “str” denote the string function, i.e., given any integer s, the function str(s) casts it into a string. For example, s = 12345678 becomes str(s) =“12345678”. Set the target t to:

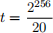
Let H be the SHA-256 hash function. Let r be a counter starting from 0. Finally, let “||” denote string concatenation.

(a) Implement a program that tries successive values of r, i.e., r = 0, 1, 2, 3, . . ., computes H(str(s)||str(r)), compares it with t and halts whenever H(str(s)||str(r)) < t, with the output r. You need to provide the program and the output r. (5 marks)

(b) Let us call the program from part (a) as: PuzzleFinder(s, t). Write a program that calls PuzzleFinder with successive inputs (s + i, t), for i = 0 to 999, and records the output for each of these 1,000 runs. What is the average number of attempts before you found the target? You need to provide your program. (3 marks)

(c) If you drew random values between 0 and 2²⁵⁵ inclusive, how many attempts on average it would take before you find a value below the target? Compare this number to the answer obtained in part (b). What does it tell you about SHA-256? (2 marks)

References

[DDN03] Danny Dolev, Cynthia Dwork, and Moni Naor. Nonmalleable cryptography. SIAM review, 45(4):727–784, 2003.

[NBF+16] Arvind Narayanan, Joseph Bonneau, Edward Felten, Andrew Miller, and Steven Goldfeder. Bit-coin and cryptocurrency technologies: a comprehensive introduction. Princeton University Press, 2016.

[Sma16] Nigel P Smart. Cryptography made simple, volume 481. Springer, 2016.