关键词 > MATH-UA.140

MATH-UA.140-023 Assignment 8

发布时间：2023-11-30

Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH-UA.140-023

Assignment 8

Due at 23:59 on Friday, December 1 .

1. This first question is about bases. Recall that a basis of Rn is a linearly independent

family of vectors that spans all of Rn. Any basis of Rn is made of exactly n vectors.

(a) Assume that we have a basis {v1 , v2 , . . . , vn } of Rn and a vector w ∈ Rm. This implies that w ∈ span{v1 , v2 , . . . , vn } and hence that there exist at least one choice of numbers α1 , α2 , . . . , αn such that

w = α1 v1 + α2 v2 + · · · + αnvn.

Show that this choice of α1 , α2 , . . . , αn is uniquely determined by {v1 , v2 , . . . , vn } and w.

Hint: Suppose that there exists a different choice, say β1 , β2 , . . . , βn such that

w = β1 v1 + β2 v2 + · · · + βnvn ,

and show that this leads to a contradiction to one of the assumptions

(b) Consider the n-by-n matrix J whose columns are the basis vectors v1 , v2 , . . . , vn respectively. Explain why J is necessarily invertible.

(c) The equation JJ- 1 = I can be seen as n equations, one for each column of the result of JJ- 1 : the first one says that a certain combination of the columns of J gives the first column of I, the second one says that a certain combination of the columns of J gives the second column of I, and so on. Using the notation

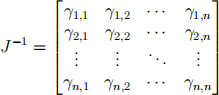
and the above observation, write down a combination of the basis vectors v1 , v2 , . . . , vn that yields the i-th standard basis vector, ei. Explain your reasoning.

2. Recall that the real eigenvalues of the 2-by-2 matrix

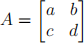
are the real values of λ such that

0 = det[A − λI].

(a) Write the det[A − λI] as a polynomial in the form

αλ2 + βλ + γ .

for some real numbers α , β, and γ expressed in terms of a, b, c and d.

(b) What are the conditions on real numbers α , β, and γ for a polynomial of the form

αλ2 + βλ + γ

to have:

1. no real zero,

2. exactly one real zero,

3. two distinct real zeros.

(d) Use the above to find examples of:

1. a 2-by-2 matrix with no real eigenvalue,

2. a 2-by-2 matrix with exactly one real eigenvalue,

3. a 2-by-2 matrix with two distinct real eigenvalues.

3. For each proposed matrix find all the eigenvalues (if there are any), and provide one eigenvector for each eigenvalue.

(a) The matrix

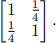
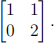
(b) The matrix

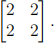
4. Consider a 3-by-3 matrix B. Computing det[B − λI] gives a polynomial of degree 3 of the form

−λ3 + β2 λ2 + β1 λ + β0

for some real numbers β2 , β1 and β0 — you do not need to show this.

(a) Exploring the limiting behaviour of this polynomial as λ gets very positive (tends to ∞) and as λ very negative (tends to −∞), what do you think conditions on β2 , β1 and β0 are needed for the polynomial to have at least one real zero.

(b) Find an example of a 3-by-3 matrix with exactly one real eigenvalue.