关键词 > EE3008A/B
EE3008A/B Linear Systems and Signal Processing Lab 2
发布时间:2023-11-28
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
EE3008A/B Linear Systems and Signal Processing
Lab 2
In this lab, we are going to explore how noise affects the detection accuracy of a digital signal using binary and general Quadrature Amplitude Modulation (QAM) format. The entire process is illustrated in the following diagram.

1. Generate a vector v that contains 100000 random bits of 1 or -1. Set
v = 2*randi([0 1],1,100000)-1;
2. Generate the digital waveform s: Let the bit period be 50 ps i.e. 20 Gbits/s and NRZ pulse shape is used. Let there be 10 samples/bit in this simulation i.e. the samples are spaced 5 ps apart and s is 10 times longer than v. Each bit in v is multiplied to 10 samples in s.
3. Add Gaussian noise to s using the function:
y = s+sigma_noise*randn(size(s));
To calculate the correct noise variance Var_noise = (sigma_noise)2 for a given SNR (in dB), perform the following steps:
1) Calculate the signal power by
Ps = mean(s.^2);
2) Since Ps/Var_noise = SNR (in linear units), we can calculate Var_noise for a given SNR (in dB) by
Var_noise = Ps/(10^(SNR(in dB)/10))
Start with SNR= 5dB.
4. Get the middle 5th sample of each bit (an example is shown below where the red samples are the middle 5th sample of each bit) and make a bit decision from that sample.
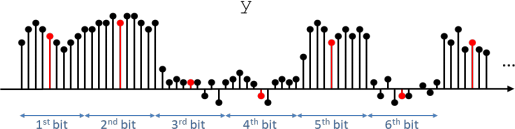
Count the number of detection errors. Calculate the BER by
BER = number of detection errors/total number of bits
5. Repeat steps 3 and 4 with SNR = 7, 9, 11, 13, 15, 17.
6. Plot the SNR-BER plot. use the function semilogy( ) to plot the curve.
7. Now, consider passing s into a channel that is characterized as an ideal low-pass filter with bandwidth 13, 10 or 9 GHz (you can refer back to Matlab Hw 2 on how to pass a signal into an ideal low-pass filter) as shown below. Let the channel output be u so that the noisy received signal is
y = u+sigma_noise*randn(size(u));
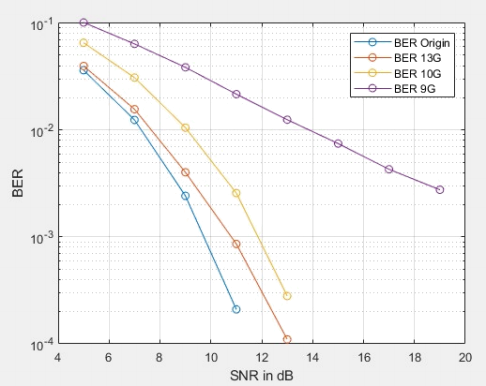
For each filter bandwidth, repeat step 3 to 6 and plot the BER vs SNR curve on the same graph. You should get a figure similar to the one shown below.

8. Repeat steps 1 to 6 (no need to repeat step 7) with polar NRZ 4-PAM signals. In this case, you have to calculate the values of the 4 levels so that the average power of v is 1. When calculating the BER, you can assume the BER = Symbol error ratio(SER)/2.
semilogy( )creates a plot using a base 10 logarithmic scale for the y-axis and a linear scale for the x-axis. A sample figure is shown below.
Questions to answer and submit:
1) How does the BER generally change with SNR? Explain this trend.
2) Is 100000 bits enough to simulate the BER when SNR = 15 or 17 dB? Explain why or why not.
3) How does the BER changes with bandwidth of the low-pass filter in step 7? Explain this trend.
4) What are the detection threshold values for the PAM-4 signals in step 8?
5) In our simulations the lowest SNR = 5 dB. What will the BER become if the SNR become even smaller?

