关键词 > CO673/CS794
CO673/CS794 : Optimization for Data Science Fall 2023 Problem Set 4
发布时间:2023-11-02
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CO673/CS794 : Optimization for Data Science
Fall 2023
Problem Set 4
Handed out: 2023-10-23.
Due: 2023-11-1, 4pm EDT, on Crowdmark. Papers must be handed in on-line using the labeled dropbox on Crowdmark. Each question is handed in as a separate upload. You can either prepare your solutions electronically using, e.g., LaTeX, or else you can hand-write them and submit a scan. In the latter case, please take care that the scan is of good quality with a white background.
Your papers may be handed in up to 24 hours late, in which case there is a 10% late penalty. Please use the late-paper dropbox on Crowdmark if you are handing in a late paper.
You may hand in some questions on time and others late. In this case, use the on-time dropbox for the on-time questions and the late dropbox for the late questions. However, you may not split the parts of a question (i.e., (a), (b), etc.) between the two dropboxes.
Collaboration policy. This problem set is a team effort. Students should hand in a single paper from each team. Team sizes should be 1–3. Students are allowed to discuss question with those in other teams in general terms including helping each other on Piazza.
However, no student should share an entire solution to a question outside their team. Note: The squared triangle inequality is:
∥a + b∥2 ≤ 2∥a∥2 + 2∥b∥2 .
It can be proved by squaring the usual triangle inequality and then applying the AGM inequality.
1. Let a1 , . . . , aN be data points in Rn. Consider
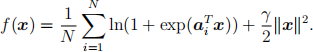
Note that m = γ for this function, as noted in PS3.
(a) Write down a formula for Δf(x). Refer to PS3.
(b) Determine an upper bound on ∥x* ∥2 . Use the symbol a(¯) to stand for the average (a1 + ··· + aN )/N in your solution. Suggested approach: This function is strongly convex with modulus γ. Therefore, inequality (3.13) of the text (also proved in lecture) is applicable, taking x = 0 in the inequality.
(c) Workout Lg(2) and B2 for f(x) as in (5.19) of the text. Use the symbol A2 to stand for maxi=1,...,N ∥ai ∥2 in your answer.
Suggested approach: Write the formula for the stochastic gradient, which has two terms, say T1 + T2 . The squared triangle inequality therefore can be used to bound the square norm of the stochastic gradient in terms of IT1 I2 , IT2 I2. Use the squared triangle inequality again to upper-bound T2 = constIxI2 in terms of Ix - x* I2 , Ix* I2 (the latter known from part (b)), and γ . This determines Lg(2) and one term in B2 . Upper-bound T1 in terms of A2 , and add this contribution as another term in B2 .
2. The Polyak stepsize αk for GD is given by the formula
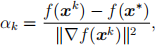
where f is the objective function. (Assume xk is not a minimizer so that the fraction is well-defined. Note that the Polyak step size requires an estimate for f(x* ), which can be restrictive in practice.) Suppose f(x) = xTHx/2+gT x, H symmetric positive semidefinite, g e Range(H).
(a) Write both the numerator and denominator of the Polyak stepsize in terms of xk - x* rather than xk and x* separately. Suggested approach: substitute for g using the equation Hx* = -g in both the numerator and denominator.
(b) [Corrected on 2023-10-23 to insert missing factor of 2.] Show that
αk e [1/(2λmax (H)), 1/(2λm(+)in (H))],
where λmax denotes the maximum eigenvalue and λm(+)in denotes the minimum positive
eigenvalue of H. Suggested approach: Write H = QDQT and substitute v := QT (xk - x* ).
(c) Show that Ixk+1 - x* I2 三 Ixk - x* I2 , where xk+1 := xk - αk Δf(xk ), αk being the Polyak step size. Suggested approach: Start with the identity Ia - bI2 = IaI2 - 2aTb + IbI2 for well-chosen a and b. Remove g from all expressions as in (a) and (b), and you should find that almost all factors will cancel out.
3. Let a e Rn / {0} and γ > 0 be given. Develop a fast code to minimize f(x) = ln(1+exp(aTx))+γIxI2 /2 in one of Matlab, Julia, Python, or R. The input arguments should be aTa and γ; it should return the computed minimal value f(x* ) (not x* ).
Suggested approach: We already know f is smooth and strongly convex from PS3, so we need only solve the equation Δf(x) = 0. Work out a formula for the gradient as in Q1. Then make the observation that the optimizer must have the form x* = -θa for some θ > 0. (Why?) This reduces the problem of solving Δf(x) = 0 to solving a univariate equation for θ. After a rescaling to change variables from θ to µ, you should arrive at the nonlinear equation ψ(µ) = 0, where ψ(µ) = µ+µexp(µ) - c, where c > 0 depends on aTa and γ . This nonlinear equation may be solved almost exactly with five iterations of Newton’s method:
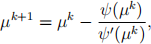
provided that the starting point µ0 is sufficiently close to the root. To find a good starting point, precompute a table of values (i,i+iexp(i)) for i = 0 : 20 (“precompute” means to store the table in your code as a literal array). Find c between two values in the second column of your table, and then linearly interpolate a starting guess µ0 using the two corresponding entries in the first column of the table.
Further notes: The inner statements of the Newton loop should compute exp(µk ) only once for more efficiency. I have put some solved values off(x* ) for various choice aT a and γ on the course website to check your code.
Hand in: derivation of the equation for µ above and code listing.
4. Write a code in Matlab, Python, Julia, or R that trains a linear binary classifier using SGD to distinguish handwritten ‘1’ digits from handwritten ‘3’ digits.
Download the MNIST handwritten digit data sample. This data set consists of hand- written digits, 0 to 9, represented as pixelated images. The original is available from
http://yann. lecun. com/exdb/mnist/
However, I found a version of the data on github that has been preformatted as a Matlab data (.mat) file. Note: to use the Matlab data, you need to convert the uint8 matrices to ordinary matrices using the double function. If you use one of the other languages, you will probably also find the data preformatted somewhere on the internet since this is a very popular data set.
The MNIST data consists of two matrices, trainx and testx, and two vectors trainy and testy. The matrix trainx contains 60000 samples, each represented as 784 pixels (28 × 28). The vector trainy has 60000 entries that are the correct labels (0 to 9) of the corresponding digits. The matrix testx and vector testy have similar formats.
First, write a function that reformats the data suitable for this question. Its calling sequence should be:
[trainXr, testXr, trainYr, testYr] = prepare mnist(dig1, dig2)![]()
The two arguments are digits to extract, which should be dig1=1 and dig2=3 for this problem set.
This routine should first read the MNIST data from a file. Then it extracts the columns of trainX and testX that correspond to entries of trainY and testY that equal dig1 or dig2.
Next, the routine finds the average value of all pixels across all images in the extracted images; say this average is q. Then append a 785th entry to each image whose value is exactly q. This entry allows the binary classifier to have an offset term.
Next, the routine should flip the signs of the augmented data items that correspond to dig1 (but not dig2). This trick allows the objective function to be written exactly as in the form of Q1. (In other words, we don’t need to treat the yi = −1 class and the yi = 1 class with separate formulas in the objective function as was done in lecture.) Call the data set with the appended q and with some flipped signs a(ˆ)1 , . . . , a(ˆ)12873 .
The routine returns: trainXr, which is the data set constructed in the last two para- graphs, testXr, which is the data set constructed from the MNIST data using the same procedure (but don’t recompute q), trainYr, a vector of labels for the columns of trainXr (i.e., each entry is equal to either dig1 or dig2), and trainYr, a vector of labels for the columns of testXr.
When I invoke the above function with dig1=1 and dig2=3, I get back the follow items:
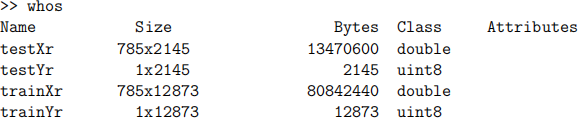
Next, write the following function:
xopt = sgd logistic(trainXr, gamma, stepsizefunc, numit)![]()
This function applies SGD to minimize the regularized logistic regression to train a linear separation model on this data. Here, trainXr contains the a(ˆ)i ’s, γ is the regularization parameter, stepsizefunc is discussed below, and numit is the number of iterations. Unlike PS3, we will not try to factor the code into separate optimization and objective functions because many properties besides the gradient of the objective function are needed by SGD in this problem.
A good classifier x will be able to distinguish 1’s from 3’s. This is equivalent toa i(ˆT)x < 0
for the vector x produced by sgd logistic for almost all of the i = 1![]() , . . . , 12873
, . . . , 12873
Note: Matlab and Julia both store entries of an m×n matrix in memory order A(1, 1), A(2, 1), ..., A(m,1), A(1, 2), A(2, 2), etc., which is called “column major” order. This means that it is more efficient in these languages to access one column of a matrix versus one row, since the entries of the same row are scattered across memory. I’m not sure whether Python or R use row-major or column-major ordering. If you are using a language with row-major order, then your code will be more efficient if you store the training set as a 12873 × 785 matrix, and similarly for test set and SVS set discussed later.
Use regularization parameter γ = 2.0.
The argument stepsizefunc is a function of the following form:
alpha = ϕ(a, x, k, gamma)
There is no named function ϕ explicitly coded like this; instead, your code should con- struct an anonymous function ϕ with this calling sequence to be passed to sgd logistic![]() . As usual, please avoid global variables.
. As usual, please avoid global variables.
Try four different step sizes, i.e., four different ways to code ϕ. The first two ways are
constant step sizes: 10 −2m/Lg(2), 10−5m/Lg(2) . (The theoretical upper limit on step size
is 2m/Lg(2), but this step size is much too big for this problem.) Note that ϕ in these
two case will be an anonymous function that uses the gamma argument (because both
m = γ and Lg(2) depends on γ), and it will ignore the other three arguments.
The third way is to use the formula
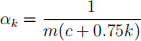
proposed in lecture, with c = Lg(2)/m2. This step size depends on k and γ but not a nor x.
The fourth step size is the stochastic Polya stepsize (Loizou, Vaswani, Laradji, Lacoste- Julien, 2021), which is coded as a function with the following calling sequence:
alpha = stoch polyak(a, x, gamma, gammab)![]()
and defined as follows. Let a denote the column of trainXr chosen on the current SGD iteration (one of thata(ˆ)i ’sdiscussed earlier). The stochastic Polya stepsize is then
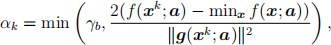
where γb ≫ 0 is another parameter. The term minx f(x;a) in the numerator should be computed using your solution to Q3. The ϕ function passed to sgd logistic should![]() wrap stoch polyak
wrap stoch polyak![]() . In particular, gammab needs to be enclosed in the anonymous function. Note that this way to factor the code creates an inefficiency because exp(aTx)
. In particular, gammab needs to be enclosed in the anonymous function. Note that this way to factor the code creates an inefficiency because exp(aTx)
is computed once in sgd logistic and a second time in stoch polyak![]()
![]() . There is a way to avoid this with more complicated coding, but we will just leave it for now.
. There is a way to avoid this with more complicated coding, but we will just leave it for now.
Set γb = 104 in your driver.
Run SGD with all four step size choices for both numit = 50 and numit = 5000 iterations.
The return variable from SGD should be the average value of x over all iterations. We did not discuss averaging the iterates in lecture, but it is commonly used in the literature and significantly reduces the variability of the results. Note that returning the average value means that a running total of the xk ’s so far must be maintained by sgd logistic![]() .
.
There are eight parameter sets total to compute x: four different step sizes, and two different iterations numbers for each step size. For each of these eight parameter sets, make three runs. [The next sentence was corrected on 2023-10-25.] Report on the min, max, and mean of the train error and (separately) the test error across the three runs. The train error is defined to be the fraction of data in the training set (trainXr) such that a i(ˆT)x is nonnegative (i.e., wrong classification), where x is the output from sgd logistic![]() .
.
The test error is the same error reported on the the test set. Construct the test set using the same procedure described for the training set using the given data testX and trainY.
Display the image of amisclassified digit for one of the 24 runs. This should be a 28×28 grayscale image. The image should be labeled with text that indicates actual value of the digit and what it was misclassified as. (All the languages have functions to make an image and paste a text label on it.) I recommend that you use the following run (out the 24): step size choice 2 (i.e., α = 10−5m/Lg(2)), 5000 iterations, first randomized trial.
Write a script that automates the whole process, i.e., does all the runs, reports all the results, and makes the requested image.
Hand in: listings of all codes, the min/max/mean fraction-wrong you achieved for each step size and for both numbers of iterations for both train and test. So in other words, your output will contain 4 × 2 × 3 × 2 numbers, neatly labeled and organized. Finally, it should include the image of the misclassified digit.
Remark: In statistics, it is sometimes advised not to apply regularization to the offset term. In other words, γ∥x(1 : 784)∥2 /2 may be a preferable regularization versus γ∥x∥2 /2 for this question. However, this change requires redoing our theory (since γ∥x(1 : 784)∥2 /2 is not strongly convex) and does not make much difference in the answer, so we will use γ∥x∥2 /2 as regularizer.
In most of my runs in both Q4 and Q5, the error for both train and test was below 5%.
5. With the same setup as in Q4, write a new function whose calling sequence is:
[xopt,numit] = sgd logistic svs(trainX, gamma, stepsizefunction,![]()
![]() . . . maxit, svsX)
. . . maxit, svsX)
Set maxit to a very large number, say 106. This is a safeguard in case the termination test discussed in the next paragraphs fails.
Instead of specifying the number of iterations in advance, this code will use a termi- nation test based on svsX (“small validation set”). Here svsX is another set of data instances, say a 785 × s matrix.
The termination test is as follows: on every sth iteration, say iteration k = js for some
integer j, we score the the average value of x1 , . . . , xk , call it xa(k)ve , against the small
validation set. In other words, we count how many data items of the small validation
set are wrongly classified by this average. If the number of wrongly classified items stays the same or goes up compared to the previous such count made on iteration
(j − 1)s using x![]() 1)s, then this indicates stagnation, and SGD should be terminated.
1)s, then this indicates stagnation, and SGD should be terminated.
Note that this test is carried out only every sth iteration because the test requires
an inner product between the each column of svsX and xa(k)ve , which is expensive. By
carrying out the test every sth iterations, the cost of the termination test is amortized across s iterations and hence is only a constant factor more than SGD without the termination test.
Write a code for SGD with this termination test. Obtain svsX by taking the first 250 entries of testXr associated with the dig1 together with the first 250 entries of testXr associated with the digit dig2. Thus, s = 500. Note that the SVS used for termination testing should not be the same data items used for computing the test score on the converged solution because this introduces bias into the test score. Therefore, the items in testX used for the termination test should be deleted from testX before using it for computing test scores.
Write a script to automate the whole question.
Run this test for all four step sizes in Q4, and three trials per step size. Report the min, mean, and max fraction wrong. Report also the min, mean, and max number of iterations before termination. (The number of iterations should always be a multiple of s if your code is correct.) Thus, you are reporting 9 numbers (min/max/mean of numit/train error/test error) over four step-size choices, so your output should have a total of 36 numbers neatly labeled and arranged. Hand in listings of all codes and the requested output.

