ECON6001/6701 Microeconomic Analysis 1, S2 2022 Problem Set 4

1. Take the “Duality” flow diagram given in your Lecture 4 slides. Verify  the entire diagram for the CES utility function

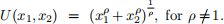
(You may take as given that this function is strictly quasi-concave).

2. Using the expressions you obtain in the previous question, verify that the equation for the substitution term ( the sij  entry in Slutsky matrix) holds. That is compute the RHS and the LHS of the following equation and verify that it is satisfied.

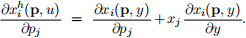
Is the income effect always positive?

3.  Consider following five observations of price - quantity pairs

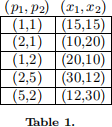
a. Explain why this data is consistent with a consumer maximizing a concave utilty function. (You might find it helpful to construct a 55 matrix of expenditures).

b.  Plot all consumption points and the budget lines on a graph paper.  Using the Weak Axiom and the Generalized Axiom of Revealed Preference, indicate the shaded region through which the indifference curve passing through (15; 15) (the first consumption choice), might lie.

4. In terms of an expenditure function e(p; u),   we  may write  (See pg 10, Lec 4 slides for example)  compensating and equivalent variations as

CV  =  e(p0 ; u0) ¡e(p1 ; u0)

EV  =  e(p0 ; u1) ¡e(p1 ; u1)

where (p0 ; u0) and (p1 ; u1) are the initial and final price/utilty pairs.

For the utility functions given in Q1 above, check the relation between CV, EV and consumer surplus.  (Hint: Do not use brute force. By duality, we need only compare the areas under Hicksian demand and Marshallian demand functions. Your answer to Q2 may help.)