553.662 Project 1; Gradient Descent. Spring 2023

• You must type your answers (using, e.g., LateX or MS Word) and return them in a pdf file. A 5% penalty will be applied otherwise.

• A solution in the form of a program output, or a Jupyter notebook output, is not acceptable.

• You must provide your program sources. They must be added as a separate file (possibly zipped), sep- arated from your answers to the questions.  They will not graded (so no direct credit for them), but not

providing them will result in a zero grade in questions that use them.

The program sources will be useful in order to understand why results are not correct (and decide whether partial credit can be given) and to ensure that your work is original.

You may use any programming language, although Python is strongly recommended. A Jupyter notebook is also acceptable as a program source.

•  Late return policy. Papers will be accepted until February 27 without penalty. After this date, papers will be accepted with a 5% penalty on the grade until one week after the due date. No paper will be accepted after that extra week.

•  Data files. The “.csv” files associated with this project are available on Blackboard.

Problem 1

Define points z1, . . . , z4 e R2 by

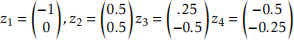
and let

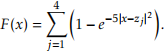
(1) Give the expressions of ⅤF and Ⅴ2F as functions of x.

(2) Compute (numerically) Ⅴ2F(x) at x =『  │0(0) and prove that F is not a convex function.

(3) Provide a surface plot of the function F over 尬 = [-1, 1]2 (use the python code“surf plot example.py” as an example).

(4) Take x =『  │0(0) . Fix c1 = 0.01 and c2 = 0.9. Provide the following three plots:

• The function t :二 F(x - tⅤF(x)) discretized over t e [-1, 1] using two colors indicating whether t satis- fies the condition

F (x - tⅤF(x)) s F(x) - c1tlⅤF(x)l2

or not.

• The function t :二 F(x - tⅤF(x)) discretized over t e [-1, 1] using two colors indicating whether t satis- fies the condition

F (x - tⅤF(x)) s F(x) - c1tlⅤF(x)l2, ⅤF(x - tⅤF(x))T ⅤF(x) s c2lⅤF(x)l2

or not.

• The function t :二 F(x - tⅤF(x)) discretized over t e [-1, 1] using two colors indicating whether t satis- fies the condition

F (x - tⅤF(x)) s F(x) - c1tlⅤF(x)l2, lⅤF(x - tⅤF(x))l s c2lⅤF(x)l2

or not.

(Use at least 200 points in the discretization of [-1, 1].)

(5) Same question with x = │ .

Problem 2

(1) Define the function f : (R2)3 二 R by

f (x1,x2,x3) = det([x2 -x1,x3 -x1]).

Using the notation 『u(-v)│ prove that

df (x1,x2,x3) = h 1(T)(x3 -x2)l + h2(T)(x1 -x3)l + h3(T)(x2 -x1)l

and

Ⅴf (x1,x2,x3) = [(x3 -x2)l, (x1 -x3)l, (x2 -x1)l]

where elements (h1,h2,h3) e (R2)3 are identified with 2 × 3 matrices [h1,h2,h3].

(2) Let 尬0 = |[x1,x2,x3] e (R2)3 : f (x1,x2,x3) > 0). Define, on 尬0

g(x1,x2,x3) = (logf (x1,x2,x3) - c)2

where c is a positive number. Compute Ⅴg(x1,x2,x3) for (x1,x2,x3) e 尬0.

(3) Let F = |(i1,j1,k1), . . . , (im,jm,km)) be a family of triples of integers with 1 s iq,jq,kq s n, where m and n are fixed integers. Let 尬F c (R2)n contain all (x1, . . . ,xn) such that (xiq,xjq,xkq ) e 尬0 for q = 1, . . . ,m.

Given elements (z1, . . . ,zn) e 尬F and numbers (c1, . . . ,cn) in (0, +o)n , we define the function F on 尬F by

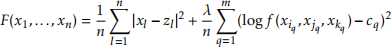
where λ is a positive number. Prove that

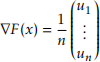
with

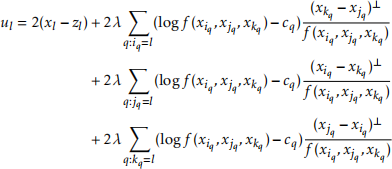
(4) Take for this question λ = 0.01.

Program a function (e.g., in Python) that takes as input a set of points x (as an n × 2 array), the list of triples F (as an m × 3 array of integers), the “target”set of points z (as an n × 2 array) and a collection of positive numbers (c1, . . . ,cn) (as an n × 1 array and returns F (x) and ⅤF(x). You code should test whether x e 尬F and return F (x) = o and ⅤF(x) = None if this is not true.

To assess the correctness ofyour function use the datasets“z.csv”, which provides (z1, . . . ,zn),“triples.csv”, which provides the family F (with indexes starting at 0) and“y.csv”, which provides a second family of points y1, . . . ,yn . You will use the latter family to compute cq= logf (yiq,yjq,ykq ).

Provide (with six decimal values) the numerical values of F(x) for x = y + ρ(z -y)) for ρ = 0, 0.1, 0.25, 0.5. (The value for ρ = 0.05 is 0.274074.)

To assess the correctness of your gradient, let e = 10-8 and use the n × 2 array h provided in the file “random direction.csv”to return, for ρ = 0, 0.1, 0.25, the values of

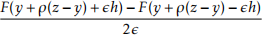
and of hT ⅤF((y + ρ(z -y)) with 6 decimal digits. (The two values should coincide.)

(5) Using α = 0.01, program gradient descent iterations with constant steps x(t + 1) = x(t) - αⅤF(x(t))

initialized at x(0) = y and over T = 105 iterations. Provide the numerical value of F(x(T )) and a plot of F (x(t)) as a function of t for t = 0, . . . , 105.

Also provide a figure containing:

(i) A scatter plot of z1, . . . ,zn .

(ii) A scatter plot of y1, . . . ,yn with all triangles (yiq,yjq,ykq ).

(iii) A scatter plot of x1(T ), . . . ,xn(T ) with all triangles (xiq (T ),xjq (T ),xkq (T )).

Make sure to label and use di佐erent colors for (i), (ii) and (iii).