关键词 > Python代写
Week 9 Tutorial Sheet (Solutions)
发布时间:2021-05-24
Week 9 Tutorial Sheet
(Solutions)
Useful advice: The following solutions pertain to the theoretical problems given in the tutorial classes. You are strongly advised to attempt the problems thoroughly before looking at these solutions. Simply reading the solu-tions without thinking about the problems will rob you of the practice required to be able to solve complicated problems on your own. You will perform poorly on the exam if you simply attempt to memorise solutions to the tutorial problems. Thinking about a problem, even if you do not solve it will greatly increase your understanding of the underlying concepts. Solutions are typically not provided for Python implementation questions. In some cases, psuedocode may be provided where it illustrates a particular useful concept.
Assessed Preparation
Problem 1. Implement a directed graph class in Python. Your graph should use an adjacency list representation and should support the following operations:
• Initialise the graph with n vertices, where n is a given parameter
• Add a directed, weighted edge between the vertices u and v, with weight w
Focus on making your code easy to use and easy to understand. Avoid using Python lists as obfuscated data struc-tures, e.g. please don’t store edges like [v1, v2,w]. It is recommended that you make an Edge class to store edges for improved readability. Writing e .u, e .v , and e .w is much nicer to read than e [0], e [1], e [2], etc, particularly once you start nesting them!
Problem 2. Label the vertices of the following graph in the order that they might be visited by a depth-first search, and by a breadth-first search, from the source s.
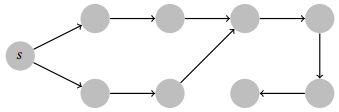
Solution
There are two possible solutions for depth-first search depending on which order you traverse the edges. One valid order is the following.
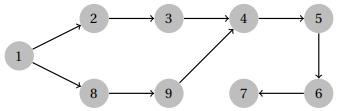
The other valid order is to visit 8 & 9 before 2 & 3. A valid order for breadth-first search is the following.
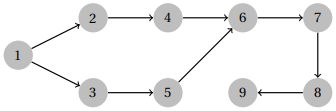
The other valid order swaps nodes 2 and 3 with each other, and nodes 4 and 5 with each other.
Problem 3. Consider an undirected connected graph G. In plain words, describe how can you use depth-first search to find whether the graph G has a cycle or not.
Solution
If at any point during depth-first search, the algorithm finds an edge that leads to a vertex which has already been visited, then there must be a cycle in the graph. For more details, see Cycle-finding in Chapter 12.3 of the unit notes.
Tutorial Problems
Problem 4. Write psuedocode for an algorithm that given a directed graph and a source vertex, returns a list of all of the vertices reachable in the graph from that source vertex. Your algorithm should run in O(V + E) time.
Solution
This problem can be solved with a depth-first search or breadth-first search. The vertices reachable from a given vertex are simply those that are visited by a search when that vertex is the starting node. So we simply perform a DFS from s and then return a list of the nodes that were visited.
1: function REACHABLE(G = (V, E), s)
2: Set visited[1..n] = False
3: DFS(S)
4: Set reachable = empty array
5: for each vertex u = 1 to n do
6: if visited[u] then
7: reachable.append(u)
8: end if
9: end for
10: return reachable
11: end function
12:
13: function DFS(u)
14: visited[u] = True
15: for each vertex v adjacent to u do
16: if not visited[v] then
17: DFS(V)
18: end if
19: end for
20: end function
Problem 5. Devise an algorithm for determining whether a given undirected graph is two-colourable. A graph is two-colourable if each vertex can be assigned a colour, black or white, such that no two adjacent vertices are the same colour. Your algorithm should run in O(V + E) time. Write psuedocode for your algorithm
Solution
To two colour a graph, the key observation to make is that once we pick a colour for a particular vertex, the colours of all of its neighbours must be the opposite. That is, once we decide on a colour for one vertex, all other reachable vertices must be set accordingly, we do not get to make any more decisions. Secondly, it does not matter whether we decide to set the first vertex to white or to black, since changing from one to the other will just swap the colour of every other vertex. With these observations in mind, we can proceed greedily.
Let’s perform depth-first search on the graph, and for each vertex, if it has not been coloured yet, select an arbitrary colour and then recursively colour all of its neighbours the opposite colour. If at any point a vertex sees that one of its neighbours has the same colour as it, we know that the graph is not two-colourable. Here is some psuedocode that implements this idea.
1: function TWO_COLOUR(G = (V, E))
2: Set colour[1..n] = null
3: for each vertex u = 1 to n do
4: if colour[u] = null then
5: if DFS(u, BLACK) = False then
6: return False
7: end if
8: end if
9: end for
10: return True, colour[1..n]
11: end function
12:
13: // Returns true if the component was successfully coloured
14: function DFS(u, c)
15: colour[u] = c
16: for each vertex v adjacent to u do
17: if colour[v] = c then // A neighbour has the same colour as us!
18: return False
19: else if colour[v] = null and DFS(v, opposite(c)) = False then
20: return False
21: end if
22: end for
23: return True
24: end function
Here, opposite(c) is a function that returns WHITE or BLACK if c is BLACK or WHITE respectively.
Problem 6. This problem is about cycle finding as discussed in Section 12.3 of the unit notes.
(a) Explain using an example why the algorithm given for finding cycles in an undirected graph does not work when applied to a directed graph
(b) Describe an algorithm based on depth-first search that determines whether a given directed graph con-tains any cycles. Your algorithm should run in O(V + E) time. Write psuedocode for your algorithm
Solution
The undirected cycle finding algorithm works by checking whether the depth-first search encounters an edge to a vertex that has already been visited. This works fine for undirected graphs, but when the graph is directed, this might yield false positives since there could be multiple paths to the same vertex with the edges in the same direction, which does not constitute a cycle. For example, the algorithm would falsely identify this as a cycle:
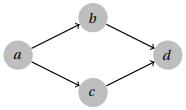
To correct this, we need to think a bit more carefully about the edges that depth-first search examines during traversal. In a different example like the following, the cycle a,b,d if identified would in fact be correct, while b, c, e, d would not.
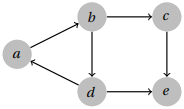
How do we distinguish between the two? Suppose that the edges traversed by the search are those de-noted in red below.
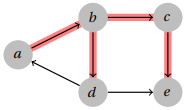
The critical observation is that when the search looks along the edge (d, e) and sees that e has already been visited, we see that the branch that visited e is a different branch than the one that visited d . Because of this, the edges will be in the same direction, and hence not a cycle. However, when the search looks along the edge (d, a) and notices that a has already been visited, we observe that a is a parent of the current branch of the search tree. This means that there is a path from a  d , and since we just discovered an edge d → a, we have found a directed cycle!
d , and since we just discovered an edge d → a, we have found a directed cycle!
So, to write an algorithm for directed cycle finding we need to perform a depth-first search and keep track of which branches of the search tree are still active, and which ones are finished. Whenever we encounter an edge to an already visited vertex, we identify it as a cycle only if the target vertex is still active, otherwise it is part of a different branch and hence not part of a cycle. Therefore instead of marking each vertex as visited or not, we will have three possible states, unvisited, inactive, and active. A vertex is active if its descendants are still being explored. Once we finish exploring a node’s descendants, we mark it as inactive. The algorithm might then look like the following
1: function CYCLE_DETECTION(G = (V, E))
2: Set status[1..n] = Unvisited
3: for each vertex u = 1 to n do
4: if status[u] == Unvisited and DFS(u) then
5: return True
6: end if
7: end for
8: return False
9: end function
10:
11: function DFS(u)
12: status[u] = Active
13: for each vertex v adjacent to u do
14: if status[v] = Active then // We found a cycle
15: return True
16: else if status[v] = Unvisited and DFS(v) = True then
17: return True
18: end if
19: end for
20: status[u] = Inactive // Finished this branch - mark as inactive
21: return False
22: end function
Problem 7. Recall from lectures that breadth-first search can be used to find single-source shortest paths on unweighted graphs, or equivalently, graphs where all edges have weight one. Consider the similar problem where instead of only having weight one, edges are now allowed to have weight zero or one. We call this the zero-one shortest path problem. Write psuedocode for an algorithm for solving this problem. Your solution should run in O(V + E) time (this means that you can not use Dijkstra’s algorithm!) [Hint: Combine ideas from breadth-first search and Dijkstra’s algorithm]
Solution
Recall that in a breadth-first search, vertices are visited in order by their distance from the source vertex. Suppose that the vertex at the front of the queue has distance d . Any unvisited adjacent vertices will be inserted into the back of the queue at distance d + 1. This implies that the queue maintained by BFS always contains vertices that are at most one distance different. In essence, the queue contains vertices on the current level at the front, and vertices on the next level at the back.
We wish to modify BFS to allow it to handle edges with zero weight. Notice that if we wish to traverse an edge of zero weight, that the target vertex will have the same distance as the current distance. Therefore we would simply like to insert this vertex not at the back, but at the front of the queue! To support this, we could use a data structure called a “deque”. A deque is short for double-ended queue, which simply means a queue that can be inserted and removed from at both ends. A deque can be implemented quite easily using a standard dynamic array. Alternatively, if you do not wish to use a deque, you can simply maintain two queues, one for the vertices at the current distance d , and one for the vertices at the next distance d + 1.
Another interpretation of this algorithm is as a modification of Dijkstra’s. Dijkstra’s algorithm would solve this problem, but in O((V + E)log(V)) complexity, which is a log factor too high due to the use of a heap-based priority queue. However, as per the observation above, the queue for this algorithm will only ever contain vertices at distance d and distance d + 1, hence we only need a priority queue that supports having at most two keys at once. Having a double-ended queue and appending the higher keys onto the end and the smaller keys onto the front satisfies this requirement.
Finally, note that unlike ordinary BFS, we also have to check the distances when visiting neighbours now since we can not guarantee that the first time we discover a vertex that we necessarily have the smallest distance (since we may discover it via a weight one edge when someone else can reach it via a weight zero edge). This is similar to how Dijkstra’s algorithm relaxes outgoing edges. A psuedocode implementation in presented below.
1: function ZERO_ONE_BFS(G = (V, E), s)
2: Set dist[1..n] = ∞
3: Set pred[1..n] = null
4: Set deque = Deque()
5: deque.push((s, 0))
6: dist[s] = 0
7: while deque is not empty do
8: u, d = deque.pop()
9: if d = dist[u] then // Ignore entries in the queue for out-of-date distances (like Dijkstra’s)
10: for each vertex v adjacent to u do
11: if dist[u] + w(u, v ) < dist[v] then
12: dist[v] = dist[u] + w(u, v )
13: pred[v] = u
14: if w(u, v ) = 0 then deque.push_front((v, dist[v])) // Add to the front of the queue
15: else deque.push_back((v, dist[v])) // Add to the back of the queue
16: end if
17: end for
18: end if
19: end while
20: end function
There are other ways to solve this problem. One very different solution is to perform a depth-first search on the graph and find all of the components that are connected by zero-weight edges. Since vertices in these components can reach each other with zero distance, they will all have the same distances in the answer, hence these components can be contracted into single vertices, and then we can perform an ordinary breadth-first search on this contracted graph.
Problem 8. Describe an algorithm for finding the shortest cycle in an unweighted, directed graph. A shortest cycle is a cycle with the minimum possible number of edges. You may need more than linear time to solve this one. Write psuedocode for your algorithm.
Solution
Since we are asking for the shortest cycle, the first thing that we should try is breadth-first search since it visits vertices in order of distance. Suppose that we run the ordinary cycle detection algorithm but using a breadth-first search in place of depth-first search. Will this find the shortest cycle for us? Unfortunately not. See the following example in which we start the search from the source s.
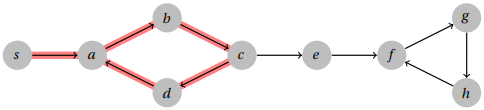
The cycle a, b, c, d is of length four and a distance of one from the source, and it will be found by the time the search reaches a distance five. However, the shortest cycle f, g, h is distance five away, and will not be found until the search reaches distance eight.
To fix this, let’s simply perform multiple breadth-first searches, one from every possible source vertex. If the source vertex is contained within a cycle of length k, then the cycle will be detected when the search reaches distance k, before any longer cycle has had a chance to be detected. By trying every possible source, we are therefore guaranteed to find the shortest cycle. This solution will take O(V (V + E)) time since we perform |V| breadth-first searches and each one takes O(V + E) time.
Notice finally that if we are searching from a vertex contained inside the shortest cycle, then the first already-visited vertex encountered will in fact be the source itself, so we can just check for that in our implementation.
1: function SHORTEST_CYCLE(G = (V, E))
2: Set best_found = ∞
3: for each vertex s = 1 to n do // Try every vertex as the source
4: best_found = min(best_found, BFS(s))
5: end for
6: return best_found
7: end function
8:
9: function BFS(s)
10: Set dist[1..n] = ∞
11: dist[s] = 0
12: Set queue = Queue()
13: queue.push(s)
14: while queue is not empty do
15: u = queue.pop()
16: for each vertex v adjacent to u do
17: if v = s then // We made it back to the source – we found a cycle!
18: return dist[u] + 1
19: else if dist[v] == ∞ then
20: dist[v] = dist[u] + 1
21: queue.push(v)
22: end if
23: end for
24: end while
25: return ∞
26: end function
Have a think about how you would solve this problem for undirected graphs. The same general ideas work, but some extra care is needed to account for some situations that do not appear in the directed case.
Supplementary Problems
Problem 9. Write psuedocode for a non-recursive implementation of depth-first search that uses a stack instead of recursion.
Solution
The function looks almost identical to the recursive version. We simply replace the recursive calls by pushing the corresponding vertex onto the stack, and loop until the stack is empty.
1: function DFS(u)
2: Create empty stack
3: stack.push(u)
4: while stack is not empty do
5: u = stack.pop()
6: visited[u] = True
7: for each vertex v adjacent to u do
8: if not visited[v] then
9: stack.push(v)
10: end if
11: end for
12: end while
13: end function
Problem 10. Write psuedocode for an algorithm that counts the number of connected components in an undi-rected graph that are cycles. A cycle is a non-empty sequence of edges (u1,u2),(u2,u3),...(uk ,u1) such that no vertex or edge is repeated.
Solution
To solve this problem, we notice that for a component to be a cycle, it must be the case that the degree (number of adjacent edges) of every vertex is exactly two. Armed with this fact, the solution to this prob-lem is to perform a depth-first search much like the ordinary connected components algorithm and add in a check to see whether the degree of a vertex is not two.
1: function COUNT_CYCLE_COMPONENTS(G = (V, E))
2: Set visited[1..n] = False
3: Set num_components = 0
4: for each vertex u = 1 to n do
5: if visited[u] == False then
6: if DFS(u) then
7: num_components = num_components + 1
8: end if
9: end if
10: end for
11: return num_components
12: end function
13:
14: // Return true if the component containing u is a simple cycle
15: function DFS(u)
16: visited[u] = True
17: Set is_cycle = True if degree(u) = 2 else False
18: for each vertex v adjacent to u do
19: if visited[v] == False then
20: if DFS(v) = False then
21: is_cycle = False
22: end if
23: end if
24: end for
25: return is_cycle
26: end function
Problem 11. In this question we consider a variant of the single-source shortest path problem, the multi-source shortest path problem. In this problem, we are given an unweighted graph and a set of many source vertices. We wish to find for every vertex v in the graph, the minimum distance to any one of the source vertices. Formally, given the sources s1,s2 ,...sk , we wish to find for every vertex v
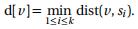
Describe how to solve this problem using a modification to breadth-first search. Your algorithm should run in O(V + E ) time.
Solution
The solution to this problem is rather simple. We perform a breadth-first search on the graph, but instead of beginning with a single vertex in the queue at distance zero, we place all of the given source vertices in the queue with distance zero. The algorithm then proceeds exactly the same. This works because the breadth-first search will discover all of the vertices that are a distance one from every source vertex before discovering vertices of distance two and so on. If a vertex has already been discovered via another source, then the breadth-first search can safely ignore it since the first source to find it must be the closest one.
An alternate solution is to add a new super source vertex to the graph and connect it to all of the given sources. After performing breadth-first search from the super source, the distances to all of the vertices will be one greater than the answer, since we had to travel along one additional edge from the super source to the real sources. Therefore we can subtract one from each of the distances and return those.
Problem 12. Recall the definition of two-colourability from Problem 5. Describe an algorithm for counting the number of valid two colourings of a given undirected graph.
Solution
First, run the algorithm from Problem 5 to check whether the graph is two colourable at all. If it is not, return zero. Otherwise, observe that after selecting a colour for a vertex, every other vertex in the same component is fixed to a particular colour. We can therefore colour each component two ways, hence the total number of possible colourings is
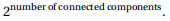
We can compute the number of connected components using depth-first search, so this algorithm takes O(V + E ) time.
Problem 13. Argue that the algorithm given in the course notes for detecting whether an undirected graph contains a cycle actually runs in O(V) time, not O(V + E) time, i.e. its complexity is independent of |E|.
Solution
If the given graph is acyclic, then E ≤ V − 1, so the ordinary depth-first search complexity of O(V + E ) is just O(V ). If instead the graph contains a cycle, then the depth-first search will find it as soon as it examines an edge to an already-visited vertex. Up until this point, none of the edges examined led to already-visited vertices, so they formed a forest of depth-first search trees, which means that there were at most V −1 of them. After we examine the cycle-producing edge, the algorithm immediately terminates, and hence it did at most O(V ) work in total.
Problem 14. (Advanced) Given a directed graph G in adjacency matrix form, determine whether it contains a “universal sink” vertex. A universal sink is a vertex v with in-degree |V|−1 and out-degree 0, ie. a vertex such that every other vertex in the graph has an edge to v , but v has no edge to any other vertex. Your algorithm should run in O(V) time. Note that this means that you can not read the entire adjacency matrix and meet the required complexity.
Solution
This problem is quite tricky, as we are not allowed to even read the entire input if we are to solve it in the required complexity. This means that we need a way to eliminate nodes from consideration very quickly. Let’s make some observations that will help. First of all, there can only be one universal sink if any, since if every vertex has an edge to v , then no other vertex has no outgoing edges. For a node to be a universal sink, it must have no outgoing edges, which means that its row in the adjacency matrix must contain all zeros. It must also have every possible incoming edge, which means that its column should contain all ones except on the main diagonal. This means that if we look at an entry A[i][j] in the adjacency matrix, we can deduce the following:
1. If A[i][j] = 1, then vertex i is definitely not a universal sink, since it has an outgoing edge
2. If A[i][j] = 0 and i
j, then vertex j is definitely not a universal sink, sink it is missing an incoming edge
This means that every time we look at an entry in the matrix (except the diagonal), we get to discard someone from consideration. This is good. We just need a way to never consider the same vertex twice, and we are in the clear. To do so, let’s start by making a linked list containing all of the vertices (this is likely the only solution in which I will ever suggest using a linked list!) We will also make an array bad[1..n] such that bad[v ] is True if we have eliminated v from consideration.
With all of this set up, we do the following. For each column of the adjacency matrix, check whether this vertex has already been discarded, and if so, move to the next column. If it has not, examine the entries in this column. If we find a 1, then mark that row as bad. If we find a 0 not on the diagonal, mark the current column as bad and move on. This is almost fast enough, except that we might scan top-to-bottom too many columns, leading to O(V2) complexity. This is where the linked list comes in. Whenever we wish to scan a column, scan only the elements presently in the linked list. When we encounter a bad vertex, remove it from the linked list so that we never have to consider it ever again. Now we only ever consider each vertex once, so the total complexity will be O(V). A universal sink exists if there is a vertex not marked as bad at the end of the algorithm.
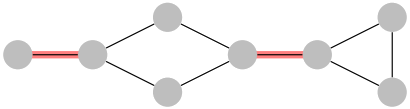
Problem 15. (Advanced) This problem is about determining another interesting property of a graph G , namely its bridges. A bridge is an edge that if removed from the graph would increase the number of connected compo-nents in the graph. For example, in the following graph, the bridges are highlighted in red.
(a) Prove that an edge is a bridge if and only if it does not lie on any simple cycle in G .
(b) Suppose that we number the vertices of G in the order that they are visited by depth-first search. Denote this quantity by dfs_ord[v] for each vertex v . Define the following quantity low_link[v] for each vertex v such that
: for any vertex u reachable from v via unused edges after visiting v
Explain how the quantity low_link can be computed in O(V + E) time
(c) Explain how the quantities dfs_num and low_link can be used to determine which edges are bridges
(d) Write psuedocode that uses the above facts to implement an algorithm based on depth-first search for determining the bridges of a given undirected graph in O(V + E) time
Solution
(a) Given a graph G, suppose that an edge e ∈ E is a bridge such that its removal would disconnect two vertices u and v . We will show that e can not lie on a cycle. Suppose for contradiction that e lies on a cycle. There was originally a path u
v that went through the edge e , ie. u
ein → eout
v . Since e is on a cycle, there is a path around the cycle ein
eout. Therefore there is a path u
ein
eout
v , hence u and v are not disconnected which is a contradiction.
Now suppose that e is not a bridge, ie. there is no pair of connected vertices u, v who can only reach each other by crossing e . We will show that e lies on a cycle. Consider the pair of vertices u = ein and v = eout. Since e is not a bridge and u and v are in the same connected component, there is a path from u to v that does not use the edge e . Since e connects u and v , we have that
is therefore a cycle.
(b) We can compute low_link by noticing that the low link of a particular vertex v is the minimum low link of all vertices adjacent to v via unused edges. This is because if we can reach vertex u via some path of length longer than one, then one of the vertices that we are adjacent to is on that path and can therefore also reach it. In other words, we can write
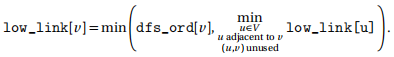
This means that at each vertex v during depth-first search, we should traverse all of our children and then update our low_link to the minimum out of all of our adjacent vertices that are connected

