CAB203

Assignment 2

This assignment is intended to give you opportunities to work with the ideas developed in the lectures. To this end, you are encouraged to discuss questions, approaches, and background material with your fellow students. However, every student must prepare and submit their own solutions. The solutions you submit must be your own. For some questions you will benefit from reading or online research. If you use sources outside of the unit you are expected to properly cite your sources. You can use any citation style you prefer, as long as you are consistent with it.

This assignment is worth 7% of your final grade.

Due date: Friday, 23 April 2021, 11:59:00pm

1   Propositional logic

1. Classify the following formula as a tautology, contradiction, contingent or satisfiable, keeping in mind that it can be more than one of these:

(A ∨ (B ∧ ¬A)) → B

(1 mark)

2. Show that ((p ∨ q) → (p ↔ q)) is a well formed formula by giving steps to show how it can be created using the rules from Lecture 4 slide 29.

(1 mark)

3. Use a truth table to show that (¬A) → B ≡ B ∨ A

(1 mark)

4. Show that ¬A → B ≡ B ∨ A by using substitutions and transitivity to chain together logical equiva-lences from Lecture 4 slides 37, 38. Indicate which logical equivalence you use at each step.

(1 mark)

5. You are working on a software project with a colleague, and over coffee she says “I was writing this if statement, and I forgot a case, so I had to fix it up, then I had it backwards around, so I had to fix it again. Now it is a complete mess. Can you help me make it easier to read?” Your colleague has written:

if not (x > 1 or (x <= 1 and x % 2 == 0)):

Your task for this question: Find the simplest formula that is logically equivalent to the formula in the if condition above.

By simplest we mean that it has the fewest logical connectives (not, and, or). Keep in mind that you can change the tests as well, eg. use != or <. For example, not (x == 1 or y > 0) is logically equivalent to x != 1 and y <= 0 and this second form has only one logical connective, so it is simpler. In fact it is not possible to write this without at least one logical connective, so this latter formula is the simplest.

(1 mark)

6. While logic is frequently portrayed as difficult to understand, in some circumstances people do it effortlessly. Consider the following to examples:

Example 1. A set of cards each have a Latin character on one side and a Greek character on the other. A new rule is imposed: cards labelled with an A on one side must have a on the other side.

On the table you see the following cards:

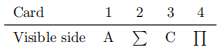
Which cards must you turn over to determine if they follow the rule?

Example 2. Alice, Bob, Charlie and Denise go to a school that rewards good behaviour by giving good students a gold star, and allowing them to take a cookie during snack times. But some children take a cookie anyway. You are given the task of finding all the cheaters who take cookies without having a gold star. At snack-time you observe the following:

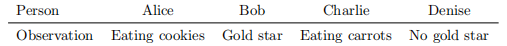
Which students do you need to have a closer look at to determine if they are cheating?

As it happens, logically these two problems are equivalent, but people frequently find one easier. Was one easier for you, and which one?

Your task for this question: answer the questions at the end of Example 1 and Example 2, and state which one you found easier. 

(1 mark)

2   Logical implication and proofs

1. Write a proof that . Use the two-column format used in Lecture 5 slide 18, specifying the steps that you are taking. Use only logical equivalences and implications found in the lectures.

(1 mark)

2. Write a Python function that takes two Boolean formulas as arguments and outputs True if the first one logically implies the second one, and False otherwise.

The Boolean formulas will be given to you as Python functions, and each will take two arguments, which are the truth values of its parameters. You don’t need to parse them or anything, just call them with truth values as parameters. So your function might look like:

def logicallyImplies(A,B):

    ...

    p = True

    q = False

    AtruthValue = A(p,q)

    BtruthValue = B(p,q)

    ...

There are further examples of similar Python functions in the solutions for Tutorial 4.

Hint: think about how you would do this with a truth table.

(1 mark)

3. A formal fallacy is a kind of problem that happens when someone tries to make a proof that doesn’t follow the rules. The invalid types that we looked at in syllogisms are a kind of formal fallacy. Very often they follow a pattern that is superficially similar to a logical implication but which is not actually a logical implication. The following example has the name denying the antecedent:

Denying the antecedent can also happen with predicate logic, as in

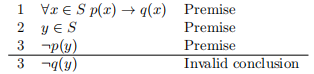
As mentioned in the lecture, in English we very often say if ... then ... sentences with an implied universal quantifier and a verbal variable. There are also a variety of ways of expressing these kinds of statements in English. Here is example:

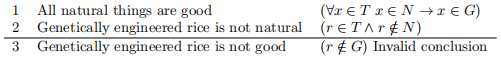
Note that this particular argument is actually a syllogism (with an invalid type), and ∀x (x ∈ S → x ∈ T) is the formal definition of S ⊆ T. Also, there is another fallacy in this argument: the appeal to nature, which is an informal fallacy.

Your task for this question: Show that denying the antecedent is a fallacy by showing that (P → Q) ∧ ¬P does not logically imply ¬Q. Do this by finding truth values for P and Q so that the left hand side is true but the right hand side is false. A truth table may be helpful, but is not required.

(1 mark)

3   Predicate logic

1. What is the truth value of ∀x ∈ {6, 8, 10} ∃y ∈ {3, 4, 7, 9} y|x?

(1 mark)

2. Use logical equivalences to find a proposition equivalent to  that uses no ∀ symbols.

(1 mark)

3. In modular arithmetic the multiplicative inverse of an integer x modulo n is an integer y that satisfies

xy ≡ 1 (mod n)

For example: the multiplicative inverse of 3 modulo 5 is 2 since 3 · 2 = 6 ≡ 1 (mod 5). Not every number has a multiplicative inverse for every modulus. For example, 3 has no multiplicative inverse modulo 6.

Your task for this question: Write a fully quantified predicate using logic and mathematical notation that says: every integer that is not a multiple of 7 has a multiplicative inverse modulo 7.

(1 mark)

4   Proof Methods

1. Suppose you are asked to prove ∀y ∈ Z ∃x ∈ Z 3x + 2y = x + 4y. Name a proof method that would be most appropriate for this task.

(1 mark)

2. Prove ∀y ∈ Z ∃x ∈ Z 3x + 2y = x + 4y

(1 mark)

3. Prove that ∀y ∈ Z ∃!x ∈ Z 3x + 2y = x + 4y. You have shown the existence part in the previous question. For this question prove uniqueness of x

(1 mark)

4. Use a proof by contradiction to show that ¬∃x ∈ Z x² + 1 = 0.

(1 mark)

5. Use a proof by contrapositive to show that ∀x ∈ Z x² + x² + 1 ≡ 0 (mod 2) → x ≡ 1 (mod 2).

(1 mark)

6. Find a counterexample to ∀x ∈ Z x² + 3x + 2 0.

(1 mark)

Submission

Sumbission process: Submission will be via Turnitin. A link will be available on Blackboard under Assessment. You can make as many submissions as you like up to the due date, but only your most recent submission will be saved. Please note that Blackboard considers the deadline to be 11:59:00pm. If your clock says 11:59pm, then it is probably past the deadline. We will generally accept these even though they are marked late, but you will get locked out at 11:59:00pm if you have a previous submission. Plan ahead and submit on time to avoid complications!

Extensions: Extension requests are processed by student services. There is a link on Blackboard under Assessment where you can apply for an extension. If you make a submission before the due date then after the due date further submissions will no longer be accepted by Turnitin. In this case you will need to email the unit coordinator ([email protected]) to delete your previous submission so that you can make a late submission.

Submission format: Your submissions must be in a format that Turnitin can read. PDF is preferred. If you would like to include hand-drawn diagrams this is acceptable, but they should be a good quality scan and easy for the marker to read. Scanners are available on campus. Other than diagrams, your submission must be typed. Program code must be selectable text, so that markers can copy/paste and see if it works; screenshots are not acceptable. Please don’t include the text of the questions, just your solutions.

Marking criteria

Each question is worth 1 mark. In most cases, a correct answer is sufficient for full marks. Questions will specifically indicate if they require you to show your work. You may receive half marks for an incorrect answer if you show your work and a reasonable method was used, i.e. if you did something which should have worked, but just made small errors. Incorrect answers without showing your work receive no marks, as will incorrect answers with work that shows an incorrect method. You may be docked marks if you don’t follow the submission format above.

Due date: Friday, 23 April 2021, 11:59:00pm

Total marks: 18