MAT00018M

UNIVERSITY OF YORK

DEPARTMENT of MATHEMATICS

Stochastic Processes B 2020-21

SUMMATIVE ASSIGNMENT

Answer ALL questions.   There are four questions; each question is worth 20 marks. 

This assignment counts for 25% of your module mark.

The deadline for this assignment is 14.00 on Monday 19th April.

Please bear in mind that your solutions should be logically complete, and contain clear explanations of your reasoning and calculations.

Your solutions must be submitted online on Moodle. If you wish to handwrite your solutions, then please scan them into one pdf file before uploading them to Moodle.

You are permitted to refer to written and online materials to aid you in your answers.

However, you must ensure that the work you submit is entirely your own, and you must not:

• communicate with other students on the topic of this assessment,

• seek assistance on this assessment from the academic and/or disability support services, such as the Writing and Language Skills Centre, Maths Skills Centre and/or Disability Services (unless you have been recommended an exam support worker in a Student Support Plan),

• seek advice or contribution from any third party, including proofreaders, friends, or family members.

We expect, and trust, that all our students will seek to maintain the integrity of the assessment, and of their awards, through ensuring that these instructions are strictly followed. Failure to adhere to these requirements will be considered a breach of the Academic Misconduct regulations, where the offences of plagiarism, breach/cheating, collusion and commissioning are relevant — see Section AM.1.2.1 of the Guide to Assessment (note that this supersedes Section 7.3).

1 (of 4).   A car insurance company employs a no-claims discount (NCD) system with the following rules:

• there are three groups, labelled 0, 1, 2;

• everybody begins in group 0;

• if a driver makes one or more claims on their policy in a year then they move down a group in the following year (or stay in group 0 if already there);

• if a driver makes no claims in a year then they move up a group in the following year (or stay in group 2 if already there);

• drivers in group 0 pay the full insurance premium (no discount), those in group 1 receive a 15% discount, and those in group 2 receive a 30% discount.

Suppose that the probability of a driver making a claim in any given year is 0.1 (no matter what group the driver is currently in, and independent of their past history of claims).

(i) Explain how a driver’s movements between groups may be described by a Markov chain on the set {0, 1, 2}; you should draw a state-space diagram and write down the corresponding transition matrix.

(ii) Find the equilibrium distribution for the chain.

(iii) Assuming that the NCD system is in equilibrium, what is the mean dis-count being given by the insurance company to its drivers?

(iv) The company is considering changing its rules so that any driver making a claim in a year moves to group 0 the following year. Explain what effect you would expect this change to have on your answer to part (iii).

2 (of 4).   A random walk Y on the integers Z has the following transition probabilities for all k ∈ Z:

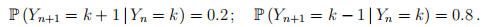
If Y0 = 30, calculate the probability that Y hits state 40 before hitting state 25.

3 (of 4).   A Markov chain X on S = {0, 1, 2, . . . } has the following transition probabili-ties:

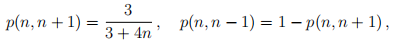
for all n ∈ S.

(i) Explain what it means for a probability distribution π on S to satisfy the detailed balance equations for X. Show that if π satisfies the detailed balance equations then π is a stationary distribution for X.

(ii) Write out the detailed balance equations for this Markov chain X. Use them to show that

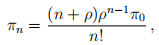
for all n ≥ 1, where ρ = 3/4, and hence determine the stationary distri-bution for X.

4 (of 4).   A Markov chain X moves between nodes labelled {1, . . . , 8} which are connected as shown in the graph below:

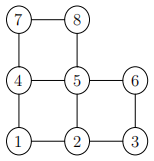
When X is at a node i, it chooses the next node to move to uniformly from those to which node i is connected by an edge of the graph. (So, for example, if X is at node 2, it next moves to one of the three adjacent nodes, each with probability 1/3.)

(i) If X0 = 2, what is the probability that X reaches node 8 before it reaches 6?

(ii) Find the unique equilibrium distribution π for X, and explain how πi is related to the degree of node i (the number of nodes to which node i is attached in the graph).

Hint: try to solve the detailed balance equations here in order to find the equilibrium distribution.