UNIVERSITY OF NEW SOUTH WALES

MATH2089 Numerical Methods

Midterm Test

Please write your full name and student ID on the first page of your submission.

Question 1. (6 marks)

Consider the equation

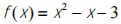
(a) Write the Newton-Raphson formula to solve this equation.

(b) Starting with 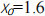, find the estimates  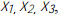using the Newton-Raphson method. Calculate the absolute error .

(c) For the starting range [1, 3] calculate the number of iterations of the bisection method required to reduce the error of solution to .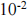

Question 2. (6 marks)

Consider the system of linear equations

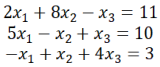
(a) Perform partial pivoting and solve this system using Gauss elimination;

(b) When we use Doolittle Decomposition to decompose a matrix into the product of lower-[L], and upper-triangular matrix, [U], the upper-triangular matrix is taken from Gauss elimination. Use your result from (a) to find [L] matrix. Explain how you would use [L] and [U] matrices to solve this system of equations. You don’t need to perform full solution.

Question 3 (5 marks)

The distance 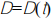traveled by an object is given in the table below:

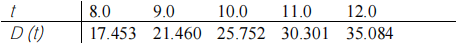
(a) Find the velocity and the acceleration at 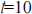using central difference approximation.

(b) Calculate the percentage relative error by comparing with exact solution for the velocity obtained from differentiation of 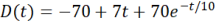 at .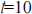

(c) Write the formula which you would use to calculate the velocity at 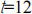to keep the same order of accuracy as a central difference.

Question 4 (7 marks)

(a) Explain the difference between Interpolation and Curve Fitting methods. Give an example where curve fitting would be more useful than interpolation.

(b) For the following data

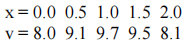
(1) Determine the location and magnitude of the maximum value of v using quadratic interpolation.

(2) Using both trapesoidal and Simpson's rule for data above, evaluate average value of 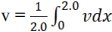. Explain the differences between your results.