Mock End of Term Examination Question Book

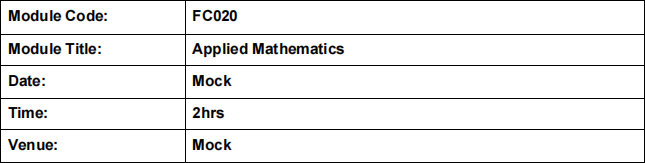
Instructions to students

1. Read all instructions very carefully

2. At the start of the examination, you should have: 

i. this question book

ii. an answer book

3. Read all of the exam questions carefully before you begin to write

4. Write your answers in the answer book.

5. Write in black or blue ink

6. Cross out any mistakes.

7. Calculators are NOT allowed in this examination.

8. Marks will be awarded where sufficient working is shown. Marks will be withheld if insufficient working is shown.

9. If you have questions at any time during the examination, you must raise your hand and wait for an invigilator. Do not attempt to communicate, by any means, with any other candidate at any time before or during the examination.

10. You may not leave the examination hall during the first hour. If the examination is less than one hour, you must stay for the entire duration of the exam (toilet breaks are permitted if necessary).

11. At the end of the exam, do not leave your seat until you have handed both the question book and the answer book and any additional sheets of paper you may have used to an invigilator, and you have been told by an invigilator that you may leave the room. 

1. Find the vector equation of the line of intersection of the planes

x + y + z = 1 and x − y + z = 1.

2. Use integration by parts to evaluate the following.

(a)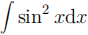 

(b)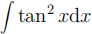 

Note. No marks will be awarded for solutions which apply the identity 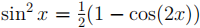, or similar.

3. Evaluate the following.

(a)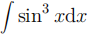 

(b)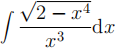 

(c)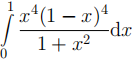 

4. Sketch the following curves and find the Cartesian equation of each.

(a)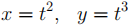 

(b)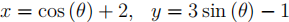 

5. Consider the function defined by .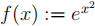

(a) Using the Maclaurin series of 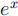, or otherwise, find the Maclaurin series of .

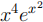(b) Hence, determine the first three terms of the Maclaurin series of the following derivative.

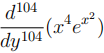
6. Use the Taylor series of sin x about an appropriate point to find an approximation for sin(3).

7. Prove that .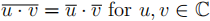

8. Find all solutions (both real and complex) to the following equation.

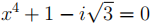
9. Let a and b be 3-dimensional vectors. Prove that .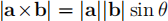

Hint. Consider 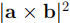and apply the dot product formula .

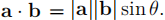10. A sphere with radius 1 m has temperature 15◦ C. It lies inside a concen-tric sphere with radius 2 m and temperature 25◦ C. The temperature T(r) at a distance r from the common center of the spheres satisfies the following differential equation.

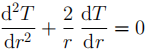
If we let S = dT/dr, then S satisfies a first-order differential equation. Solve it to find an expression for the temperature T(r) between the spheres.