comp2123                                                                        Solution 3: Trees                                                                        s1 2021

Warm-up

Problem 1. Let A be an array holding n distinct integer values. We say that a tree T is a pre-order realization of A if T holds the values in A and a pre-order traversal of T visits the values in the order they appear in A.

    Design an algorithm that given an array produces a pre-order realization of it.

Solution 1. Let T be a tree where every internal node has a right child and no left child. Such a tree is simply a path connecting the root to its only leaf and its pre-order traversal visits the nodes along the path from the root going down to its leaf. Therefore, assigning the values of A to the path from the root going down is a pre-order realization of A.

    It is worth noting that given any tree on n nodes, we can assign the values of A to its nodes such that T is a pre-order realization of A. The above construction is just easier to describe and implement.

Problem 2. Let A be an array holding n distinct integer values. We say that a tree T is a post-order realization of A if T holds the values in A and a post-order traversal of T visits the values in the order they appear in A.

    Design an algorithm that given an array produces a post-order realization of it.

Solution 2. Let T be a tree where every internal node has a right child and no left child. Such a tree is simply a path connecting the root to its only leaf and its post-order traversal visits the nodes along the path from the leaf going up towards the root. Therefore, assigning the values of A to the path from the leaf going up is a post-order realization of A.

    It is worth noting that given any tree on n nodes, we can assign the values of A to its nodes such that T is a post-order realization of A. The above construction is just easier to describe an implement.

Problem solving

Problem 3. Design a linear time algorithm that given a tree T computes for every node u in T the size of the subtree rooted at u.

Solution 3. We use a recursive helper function. When the function is called at some node u in T, we recursively compute the size of the left and right subtrees of u, add 1, set the result to be the size of the subree at u, and return the value to be reused further up in the recursion.

    We claim that the call size-helper(u) sets u.sub size to the size of the subtree rooted at u and returns this value. The correctness of this claim rests on the in-ductive assumption that the claim is true for recursive calls to smaller subtrees (the

1   def subtree-size(T)

2       def size-helper(u)

3           u.sub_size ← 1

4           for w in u.children()

5               u.sub_size ← u.sub_size + size_helper(w)

6           return u.sub_size

7       size-helper(T.root)

ones defined by the children of u) and the fact that

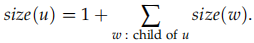
    Each call to size-helper(u) takes O(1) time, not counting the work done in recursive calls. Therefore, the total running time is O(n) time.

Problem 4. In a binary tree there is a natural ordering of the nodes on a given level of the tree, i.e., the left-to-right order that you get when you draw the tree. Design an algorithm that given a tree T and a level k, visits the nodes in level k in this natural order. Your algorithm should perform the whole traversal in O(n) time.

Solution 4. We perform an in-order traversal over all nodes in the tree, but we do not execute the visit routine on every node. Instead we keep track of the level of the node we are traversing and we call visit only when the level of the node we are currently traversing equals k.

    The extra bookkeeping needed to track the level we are at does not increase the running time of the standard in-order traversal, which is O(n).

Problem 5. Design an algorithm that given a binary tree T and a node u, returns the node that would be visited after u in a pre-order traversal.

Solution 5. If u.le f 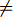t   then u.le f t is the next node. Else, if u.le f t = and u.right 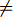 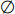then u.right is the next node. Otherwise, let v be the first ancestor of u that has a right child and v.right is not u’s ancestor (that includes u itself), then v.right is the next node. If no such node v exists then u is the last node in the traversal and there is no next node.

    The algorithm may take up to O(n) time to find the next node.

Problem 6. Design an algorithm that given a binary tree T and a node u, returns the node that would be visited after u in an in-order traversal.

Solution 6. If u.right 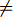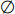then the next node is the left-most descendant of u.right (that is we follow the left child pointer until we reach a node without a left child). Else, we move to the parent of u, call it v. If we arrive at v from its left subtree, then v is the next node; otherwise, we keep updating v until we find such a node. If we happen to reach the root, then u is the last node in the traversal and there is no next node.

    The algorithm may take up to O(n) time to find the next node.

Problem 7. Design an algorithm that given a binary tree T and a node u, returns the node that would be visited after u in a post-order traversal.

Solution 7. If u does not have a parent, then u is the last node in the traversal and there is no next node. Otherwise, let v be the parent of u. If u is v’s right child, then v is the next node. If u is v’s left child and v has no right child, then v is the next node. If u is v’s left child and v has a right child, then we start a post-order traversal at v.right.

    The algorithm may take up to O(n) time to find the next node.

Problem 8. The balance factor of a node in a binary tree is the absolute difference in height between its left and right subtrees (if the left/right subtree is empty we consider its height to be -1). Design an algorithm for computing the balance factor of every node in the tree in O(n) time.

Solution 8. We use a recursive helper function that takes as input a node u and computes the balance factor at u and returns the height of the subtree rooted at u.

1   def balance(T)

2       def balance-helper(u)

3           left_height ← -1

4           right_height ← -1

5           if u.left 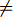 nil

6               left_height ← balance-helper(u.left)

7           if u.right 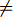 nil

8               right_height ← balance-helper(u.right)

9           u.balance ← abs(left_height - right_height)

10           return 1 + max(left_height, right_height)

11

12       balance-helper(T.root)

    We claim that balance-helper(u) sets u.balance to the balance factor at u and returns the height of u. To prove the correctness of this claim we use the induc-tive assumption that the algorithm returns the correct height for the left and right subtrees. If both are empty then balance-helper returns 0 and sets u.balance to 0, which is the correct thing to do. If one of them is non-empty we return its height plus 1 and set u.balance to its height, which again is correct. Finally, if both are non-empty, we return 1 + max(le f t height,right height) and set u.balance to |le f t height − right height|, which again is correct.

    Each call to balance-helper(u) takes O(1) time, not counting the work done in recursive calls. Therefore, the total running time is O(n) time.

Problem 9. Describe an algorithm for performing an Euler tour traversal of a binary tree that runs in linear time and does not use a stack or recursion.

Solution 9. In an Euler tour traversal of a binary tree, our current position is determined by the vertex we are at and whether we are visiting this vertex from the left, from the bottom, or from the right. We encode this position with a pair (u, W) where u is a node in the tree and W ∈ {L, B, R}. For each position the following function returns the next state.

1   def euler-next(u, W)

2       if W = "L" and u.left 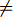nil

3           return (u.left, "L")

4       else if W = "L" and u.left = nil

5           return (u, "B")

6       else if W = "B" and u.right 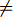nil

7           return (u.right, "L")

8       else if W = "B" and u.right = nil

9           return (u, "R")

10      else if W = "R" and u is the root

11          return "the end"

12      else if W = "R" and u = u.parent.left

13          return (u.parent, "B")

14      else if W = "R" and u = u.parent.right

15          return (u.parent, "R")

    Correctness follows directly from the definition of the Euler tour traversal.

    We only do a constant number of comparisons, so the function takes O(1) time. Since the function is executed exactly three time per node (once for each of the three states), the running time per node is O(1). Hence the total running time if O(n) for the tree.

Problem 10. For any pair of nodes in a tree there is a unique simple path (one that does not repeat vertices) connecting them. Design a linear time algorithm that finds the longest such path in a tree.

Solution 10. Here is a sketch of a solution. The longest path either connects the root and a leaf or it connects two leaves. In the first case, if the longest path connects the root to a leaf, we compute the deepest node by computing the height of every node and finding the maximum. Its height is the length of this path.

    In the second case, if we let u be the lowest common ancestor of the leaves and let v and w be the two children of u that are ancestors of these two leaves, then the length of the path is

height(v) + height(w) + 2.

Therefore, we can compute in O(n) time the heights of all subtrees and then we can find the internal vertex maximizing the above formula.

    The issue of how to find the actual path can be resolved by not only remember-ing the height of each subtree but also through which child there is a path to a leaf attaining that height.