Due: 11:59pm ET, Monday March 22, 2021

MAT224 Linear Algebra II

Assignment 4

Instructions:

Please read the Assignment Policies & FAQ document for details on submission policies, collaboration rules and academic integrity, and general instructions.

1. Submissions are only accepted by Gradescope. Do not send anything by email. Late submissions are not accepted under any circumstance. Remember you can resubmit anytime before the deadline.

2. Submit solutions using only this template PDF. Your submission should be a single pdf with your full written solutions for each question. If your solution is not written using this template PDF (scanned print or digital) then your submission will not be assessed. Organize your work neatly in the space provided. Do not submit rough work.

3. Show your work and justify your steps on every question but do not include extraneous information. Put your final answer in the box provided, if necessary. We recommend you write draft solutions on separate pages and afterwards write your polished solutions here on this template.

4. You must fill out and sign the academic integrity statement below; otherwise, you will receive zero for this assignment.

Academic Integrity Statement:

I confirm that:

• I have read and followed the policies described in the document Assignment Policies & FAQ.

• In particular, I have read and understand the rules for collaboration, and permitted resources on assignments as described in subsection II of the the aforementioned document. I have not violated these rules while completing and writing this assignment.

• I understand the consequences of violating the University’s academic integrity policies as outlined in the Code of Behaviour on Academic Matters. I have not violated them while completing and writing this assignment.

By signing this document, I agree that the statements above are true.

Signatures: 1)                                                                                                                                        

                 2)                                                                                                                                        

1. Let

1(a) Show that W is a subspace of .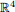

1. Let

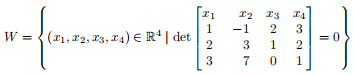
1(b) Determine dim W.

2. Let V be a vector space, and let T .

2(a) Prove that if T is injective, then 0 is not an eigenvalue of T.

2(b) Prove that if 0 is not an eigenvalue of T then T is injective.

3. Let V be a finite dimensional vector space, and let S, T ∈ L(V ).

3(a) Suppose that if λ 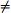0 is an eigenvalue of ST. Show that λ is also an eigenvalue of T S.

3. Let V be a finite dimensional vector space, and let S, T .

3(b) Suppose that 0 is an eigenvalue of ST. Show that 0 is also an eigenvalue of T S.