MATH 187A Introduction to Cryptography Winter 2021
MATH 187A Introduction to Cryptography Winter 2021
FINAL PROJECT
DUE MARCH 19, 2021 AT 2:30PM PST
Instructions. You may not collaborate or discuss the final projects with any humans outside of the TAs and instructors for this class. In particular, there will be no discussion on Zulip about the final project. Even if you ask the teaching staff for help, you must write the solutions on your own in your own words. The final project must be submitted through Gradescope by 2:30pm PDT on March 19, 2021 and there are no exceptions to this rule.
You will be able to look at your scanned work before submitting it. Please ensure that your submission is legible (neatly written and not too faint) or your homework may not be graded. By turning in your work, you acknowledge that the work contained in the document is your own and you did not engage in any academic misconduct. After uploading, indicate which problems are on which pages on Gradescope.
Students should consult the class notes, lecture slides, instructor, and TAs when they need help with homework. Students should not look for answers to homework problems in other texts or sources, including the internet. You may ask questions about the homework in office hours and on Zulip. However, you should only use Zulip to ask for clarifications on the homework problems. Publicly posting any part of your work on Zulip or anywhere else will be considered cheating, and the author of the post will fail the class immediately!
Your assignments in this class will be evaluated not only on the correctness of your answers, but on your ability to present your ideas clearly and logically. You should always explain how you arrived at your conclusions and justify your answers with mathematically sound reasoning. Whether you use formal proof techniques or write a more informal argument for why something is true, your answers should always be well-supported. Your goal should be to convince the reader that your results and methods are sound.
All problems have equal weight unless otherwise specified and use the conventions from lecture.
You must show all intermediate computational steps for each problem.
Key concepts: entropy, conditional entropy, Huffman tree, comma-free codes, RSA, Legendre symbol, Jacobi symbol, probabilistic primality testing.
1. (10 points) Suppose that random variables X, Y, Z are obtained by spinning the adjacent wheel, with X given by the outermost circle, Y given by the intermediate circle, and Z given by the innermost circle.
2. Suppose a random cryptosystem is obtained as follows: The message consists of two independent random variables 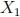 ,
, 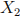 each generated by spinning a wheel with arcs labelled 0, 1, both of length 1/2. Let there be 4 equiprobable keys with the following corresponding encrypting transformations: (Draw a picture of the wheel in question if you are confused about the messages.)
each generated by spinning a wheel with arcs labelled 0, 1, both of length 1/2. Let there be 4 equiprobable keys with the following corresponding encrypting transformations: (Draw a picture of the wheel in question if you are confused about the messages.)
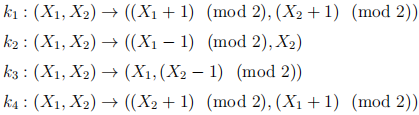
(a) (3 points) Does this system achieve perfect secrecy? Explain.
(b) (2 points) What is the probability of receiving the ciphertext 00?
(c) (3 points) Compute H(K|C).
(d) (4 points) Now suppose
,
are chosen with probability 1/8,
is chosen with probability 1/4 and
is chosen with probability 1/2. What is the probability of receiving each ciphertext? That is, calculate P(C = 00), P(C = 01), P(C = 10), P(C = 11).
(e) (4 points) What is H(K|C) if
,
are chosen with probability 1/8,
is chosen with probability 1/4 and
is chosen with probability 1/2?
3. Suppose a certain file contains only these letters with the following frequencies
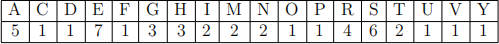
(a) (6 points) Construct the comma-free code that enables you to compress the file so that you can store it using the least number of bits.
(b) (6 points) Use the comma-free code you construct from part (a) to decrypt the following ciphertext.
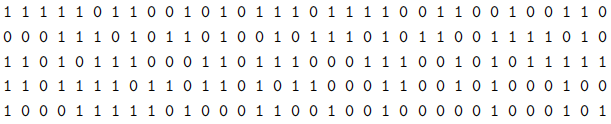
4. (a) (5 points) Compute 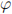 (198) and 37121(mod 198) by hand. Show all the interme-diate computational steps
(198) and 37121(mod 198) by hand. Show all the interme-diate computational steps
(b) (5 points) How many operations does it take to do compute 371027 (mod 9541717) by repeated squaring? Justify your answer.
5. Alice and Bob want to communicate in secret using RSA. Bob designs a public key as follows.
(a) (3 points) Bob chooses primes p = 53, q = 31. Compute N and(N).
(b) (4 points) Bob is considering 29 or 42 for his encryption key. Which is better? Justify your answer.
(c) (5 points) He changes his mind and chooses e = 7, so his public key becomes (N, e) = (1643, 7). Find the corresponding decryption exponent d using the Berlekamp algorithm and show all the intermediate computational steps.
(d) (2 points) What is the longest message (in letters) which Alice can send to Bob via this system? Justify your answer.
(e) (3 points) For some reason, Alice wants to send Bob the message NO. What is the numeric message m which she will encrypt?
(f) (5 points) Compute the ciphertext c achieved by encrypting the m value which you computed in part (e) via Bob’s public key. The answer should be a number. Show all the intermediate computational steps.
(g) (5 points) Bob receives the ciphertext C = 832. Compute the corresponding plaintext M (a number). Show all the intermediate computational steps.(h) (3 points) Find the corresponding letter message L (a word) to the plaintext M from part (g).
6. (10 points) Eve is trying to break an RSA message which she knows is based on the modulus N = 376037. Suppose she discovers that 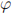 (N) = 374796. Help her recover the primes p and q such that N = pq. Justify your answer. Show all the intermediate computational steps. No exhaustive search argument or direct factoring by some piece of software will be accepted.
(N) = 374796. Help her recover the primes p and q such that N = pq. Justify your answer. Show all the intermediate computational steps. No exhaustive search argument or direct factoring by some piece of software will be accepted.
7. (a) (5 points) Give the complete list of quadratic residues modulo 41.
(b) (4 points) Does the equation x2 ≡ 11(mod 41) have a solution? Explain.
(c) (5 points) Find all solutions modulo 41 of the quadratic equation
x2 + 10x + 20 ≡ 0 (mod 41).
Hint: complete the square.
8. (a) (8 points) Compute the following Legendre symbols.
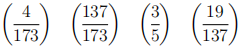
(b) (8 points) Compute the following Jacobi symbols.
J(20, 121) J(12, 175) J(9, 3490135) J(196, 387)
9. (5 points) Alice wants to determine whether p = 6246892831 is prime or not. She computes
26246892830 ≡ 3958278997 (mod 6246892831).
What can she conclude about the primality of p? Justify your answer.
10. (Bonus, 10 points) Decrypt the message
ANOITANWCIHHCANPEFERRDCARGSIETODEGNARISPERAPERDFORAMETSARANDDEVRESESONE
2021-03-19
