MAST20026 Real Analysis

Semester 1, 2021

Assignment 1

Due: Monday, 15th March (3:00pm)

Write your name and your student number in the spaces provided below.

Full working must be shown in your answers.

Assignments should be neatly handwritten in blue or black pen.

To complete this assignment you should write your solutions into the blank answer spaces following each question.

– If you have a printer (or can access one), then you should print out the assignment template, handwrite your solutions into the answer spaces and then scan your assignment to a PDF file for upload; If you do not have a printer, but you can annotate a PDF using an iPad/Android tablet/Graphics tablet, then annotate your answers directly onto the assignment PDF and save a copy for submission;

– Whether you complete on paper or by annotating the pdf, if you find you are unable to answer the whole question in the answer space provided then you can append additional handwritten solutions to the end of your template assignment. If you do this you must make a note in the correct answer space for the question, warning the marker that you have appended additional remarks at the end.

When complete, scan your assignment and upload in ‘GradeScope’.

Please note that some marks will be allocated for properly setting out your solutions and the correct use of notation.

Students must not seek or obtain help with assignment questions from others, including: fellow students, University employees or people from outside the University, whether in person or via social media (or other means of communication). Seeking, obtaining or providing such help is considered to be academic misconduct.

Posting assignment questions on internet sites is strictly forbidden.

Name:

Student ID:

The assignment begins on the next page.

1. (4 marks) A treasure hunt on the Island of Knights and Knaves:

This problem is about the Island of Knights and Knaves: see Tutorial 1A Question 1.

A knight and a knave stand guard outside two doors. Behind one door is a treasure and behind the other is nothing. The knight and the knave both know the following:

(i) the location of the treasure;

(ii) whether the other guardian is a knight or a knave;

(iii) that knights are always truthful and knaves always lie;

(iv) that their companion also knows the location of the treasure.

Seeking the treasure you arrive at the doors. You do not know which guardian is a knight and which is a knave, but you can ask one question to one of the guardians, which they will answer.

(a) Write down a question which you can ask to either of the guardians that will allow you to find the treasure.

Hint: Either you will ask your question to the knight, or you will ask it to the knave. Consider the two possible cases separately. You must find a way for one question to involve both guardians.

Remark: This question illustrates an important feature of humans and other animals: we possess and can use knowledge, not just about the physical world, but also about the knowledge and behaviours of other creatures. Solving this question requires you to use your knowledge of what the knight and the knave know about the world and each other and how they will each behave.

(b) Explain how your question will lead you to find the treasure.

2. (4 marks) A useful property of the real number zero:

Let R denote the real numbers. At school we learn that zero is a special number, which we can use to help solve equations by factorisation. Specifically, we learn the following statement:

P: If the product of two real numbers is zero, then one or other of the numbers is zero.

(a) Translate the statement P into a quantified, conditional statement in First Order Logic.

(b) Express the statement P in First Order Logic using the contrapositive to the conditional in your answer to Part(b).

(c) In fact zero is the only number with the property identified in P. Express this fact in First Order Logic.

(d) For your statement in Part (c), show how to provide examples which verify the statement for each non-zero real number.

3. (4 marks) A tautology:

Prove that is a tautology.

4. Congruences and perfect squares:

This problem extends the ideas in the proof of Theorem 1.46 from lectures.

Definition: Let 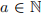be a natural number and 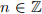an integer. For 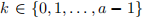, we say that n is congruent to k mod a if n = qa + k for some integer q. The number k is unique and we write n k mod a.

(The notation n k should not be confused with the use of to denote the logical equivalence of propositions).

Notation: 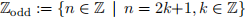denotes the set of odd integers.

(a) Translate the following statements into First Order Logic:

(i) The square of any odd integer is congruent to one 1 mod 4;

(ii) The square of no integer is congruent to 2 or 3 mod 4.

(b) Present detailed proofs of your translations of the statements from Part (a).