闪电代写 -代写CS作业_CS代写_Finance代写_Economic代写_Statistics代写_代码代做_IT代写_加急帮助

MATH 178, Spring 2021, Exam 1

Study Sheet - Key answers

Note: The topics for exam 1 are everything we have learned (up to the exam). Here are some problems to practice. The data sets are modified so you can do it with a calculator. A calculator and a 3”x5” note (both sides) can be brought to the exam.

1. Compute the Annual Percentage Yield (APY) for bank accounts which have the following cases:

(a) 0.25% interest compounded monthly

Answer: 3.04%

(b) 1.25% interest compounded quarterly (i.e. every 3 months)

Answer: 5.09%

(c) 0.025% interest compounded daily (assume non-leap year!)

Answer: 9.55%

2. Compute the interest rate for a single compound period for bank accounts with the following specifications:

(a) 7.5% APY, compounded monthly

Answer: 0.604% monthly

(b) 9.5% APY, compounded every other week (assume exactly 52 weeks per year)

Answer: 0.350% every two weeks

3. You take out a mortgage of $200000 on a condo with an interest rate of 0.75% each month. Each month you pay $1750 toward the mortage.

(a) Set up a difference equation model for the principal in month n, xn. (Don’t forget to include x0!)

Answer: xn+1 = (1.0075)xn — 1750, x0 = 200000

(b) How much principal is left on the mortgage after two months?

Answer: x2 = $199498.10

(c) What is the explicit solution of the model? Use it to compute the amount left to pay off after 10 years.

Answer: xn = (1.0075)ⁿ (200000) —

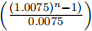
x120 = $151621.43

(d) How long will it take to pay off the mortgage? (Consider using the equation in the previous part.)

Answer: 261 months (i.e. 21 years and 9 months)

(e) How much would you have to pay each month in order to finance the mortgage on interest alone (i.e. never pay down the princi-pal)?

Answer:

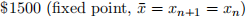
4. You take some time off to save for college. With an initial investment of $2000, you invest in an account which has an APY of 5% and compounds monthly. You agree to invest $250 in the account each month.

(a) Determine the monthly interest rate for the amount in the account.

Answer: 0.407%

(b) Set up a different equation model for the amount in the account in month n, xn.

Answer: xn+1 = (1.00407)xn + 250, x0 = 2000

(c) How much money do you have in the account in two months?

Answer: $2517.35

(d) Determine the explicit solution xn and use it to determine the amount in the account in four years. How much higher is this amount than the amount you have paid into the account in this time?

Answer:

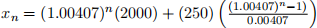
x48 = $15655.10

x48 — 8 [(48)(250) + 2000] = $1655.10

5. Rabbits and sheet interact competitively in an shared environment according the following system of difference equations:

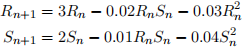
where n tracks increments of years.

(a) Explain the significance of the terms —0.02RnSn and —0.01RnSn. What physical event does it model? How does it influence the species?

Answer: This corresponds to the effect of rabbit and sheet in-teracting. The competition negatively affects both species.

(b) Determine the four fixed points of the system.

Answer:

(c) Suppose we initial have R0 = 50 and S0 = 25. Use the model to predict the population levels in one year time.

Answer: R1 = 50, S1 = 12.5

6. The weather in San Jos´e is either sunny or rainy. Suppose that, after a sunny day, there is a 30% chance of having a rainy day, and after a rainy day, there is a 50% chance of having a sunny day.

(a) Construct a difference equation model for the discrete state Markov chain, where Sn is the chance of the n^th day being sunny, and Rn is the chance of the n^th day being sunny.

Answer:

(b) Suppose today is sunny. What is the probability that the day after tomorrow is sunny?

Answer: 64%

(c) Compute the fixed point for the system.

Answer:

(d) Interpret the fixed point in terms of the long-term behavior of the system.

Answer: In the long-term 62.5% of days will be sunny and 37.5% of days will be rainy.

7. Long-term data is collected from the Rock, Paper, Scissors Champi-onship (this is a thing!):

(i) After Rock, another Rock is chosen 30% of the time, Paper is chosen 50% of the time, and Scissor is chosen 20% of the time.

(ii) After Paper, another Paper is chosen 20% of the time, Rock is chosen 20% of the time, and Scissor is chosen 60% of the time.

(iii) After Scissor, another Scissor is chosen 10% of the time, Rock is chosen 70% of the time, and Paper is chosen 20% of the time.

(a) Set up a difference equation model of the discrete time Markov chain, where Rn, Pn, and Sn are the chances of choosing a Rock, Paper, and Scissor, respectively, on the n th turn.

Answer:

(b) Suppose a player initially chooses a Rock. What is the probability that the player’s third choice if a Rock? (Note, the initial choice counts as the first choice.)

Answer: 33%

(c) Set up, but do not solve, a linear system of equations for the fixed point of the system. Write the equations in the form Ax = b where A is a 3 × 3 matrix. [For validation, the solution of the system should be Rock 38.7%, Paper 31.6%, and Scissor 29.7%.]