CSCI-PHYS 3090— Quantum Computing— Spring 2021 Problem Set #4

Due Wednesday, February 24, at 11am.

Homework is graded for clarity of explanation as much as for mere “correctness” of the final answer. You will earn partial credit much easier if your writing is legible and organized. Please scan and submit online, making sure that your scan can be easily read!

Problem 1: One-time pad encryption (30 points)

In this problem, we consider messages 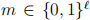for some fixed length 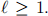The goal is to consider a special one-time pad and provide some analysis of its implication for the one-time pad scheme.

(a) For this subproblem, assume that m = 1010 · · · 10. Find a one-time pad such that m ⊕ = 0 · · · 0.

(b) Construct a one-time pad that acts as the identity on every and prove that it indeed acts as the identity.

(c) If we choose a one-time pad p uniformly, what is the probability that it is equal to  from Part (b)?

(d) Use your answer from Part (c) to explain why the one-time pad scheme is secure even if there is a nonzero probability of choosing .

Problem 2: Quantum cryptography and BB84 (40 points)

Alice and Bob are using BB84 to establish a secret key.

(a) If Alice transmits 100 bits, each randomly in either  what is the probability that Bob will be unlucky and choose to measure in the wrong basis every single time?

Eve knows that if she measures in a random basis it will disturb Alice’s transmissions and cause errors in Bob’s copy of the secret key. Then Alice and Bob will notice her eavesdrop-ping. So, she will be sneaky. Eve fixes a 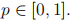 With probability p, Eve does not measure Alice’s signal. With probability 1 - p, Eve does measure Alice’s signal. If Eve measures, then with even probability, she either measures in the 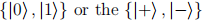basis.

(b) For any given bit of Alice’s signal, what is the probability that Eve measures Alice’s bit in the computational basis?

Consider the case when Alice transmits in the same basis that Bob measures in. We are interested in whether or not Eve attempts to intercept this transmission and how that affects the probability that Alice’s and Bob’s bits agree.

(c) Assuming that Eve does not make an attack, calculate the probability that Bob’s measurement outcome (i.e., his key bit) is different to the bit transmitted by Alice.

(d) Assuming that Eve does make an attack, calculate the probability that Bob’s measur-ment outcome is equal to the bit transmitted by Alice.

Problem 3: Impossibility of chosing a basis to identify all of Alice’s signal (30 points)

Suppose Alice sends Bob one of two states: 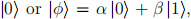with 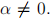Bob is going to measure to try to figure out which state Alice sent. He has his own orthogonal basis 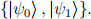He concludes that Alice prepared 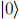if he gets outcome 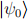and that she prepared 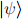if he gets outcome 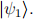Show that no matter which basis Bob measures in, he will always have some chance of misidentifying Alice’s prepared state.