Assigned February 10. Due February 19. Point values are as marked.

1. (20) Define

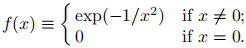
Show that 2⁽ⁿ⁾ (x) exists for all x and all n, and that f(n) (0) = 0 for all n. You may assume standard calculus facts about exponentials, polynomials, and rational functions.

2. (15) Let f : [a, b] → R be continuous, with a < b, and suppose that f′ exists (finite or infinite) everywhere on (a, b). Suppose that

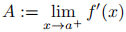
and

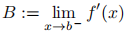
both exist as real numbers. Show that f′+(a) and f′_(b) both exist as real numbers, with A = f′+(a) and B = f′_(b).

3. (15) Let f : R → R have a derivative (finite or infinite) at all points, and suppose that

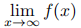
and

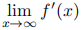
both exist as real numbers. Show that the second limit equals 0.

4. (15) Let f : R → R have a derivative (finite or infinite) at all points, and suppose that

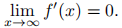
Show that the limit

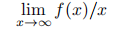
exists and equals 0.

5. (20) Suppose f : [0, 1] → R is continuous, f(0) = 0, and f′(x) exists and is finite for all x ∈ (0, 1). Suppose furthermore that f′(x) is an increasing function on (0, 1). Show that f(x)/x is also increasing on (0, 1). Give an example to show that this conclusion can fail if we remove the hypothesis that f(0) = 0.

6. (15) Let f : (0, 1) → R have a finite derivative everywhere in (0, 1), with |f′(x)| ≤ 1 ∀x ∈ (0, 1). Show that

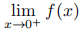
and

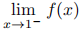
both exist as real numbers.