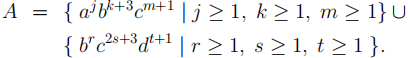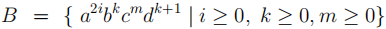CISC/CMPE 223 - Assignment 2 (section 1) (Winter 2021)

Due: Thursday February 11, 2:00 PM (Kingston time)

Regulations on assignments

• The assignments are graded according to the correctness, preciseness and legibility of the solutions. All handwritten parts, including figures, should be clear and legible. This assignment is marked out of 20 possible marks.

• Please submit your solution in onQ before the due time.

• The assignment must be based on individual work. Copying solutions from other students is a violation of academic integrity. See the course web site for more information https://research.cs.queensu.ca/home/cisc223/2013w/#AS

1. (4 marks) Using the method described in Section 9.1 and in videos of Week 3 (video no. 12) convert the following regular expression into a state diagram:

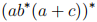
    Here the alphabet is Σ = {a, b, c}. Note that the closure operation has highest precedence so ab∗ denotes strings with one occurrence of a and zero or more occurrences of b.

    Your answer should indicate how you arrived at the result:

• As intermediate steps write down the state diagrams that you construct for subex-pressions of the given regular expression, and for each intermediate step clearly indicate which subexpression it corresponds to.

• Please do not simplify/modify the state diagrams. Simplifications/modifications of the state diagrams are considered as errors when marking (independently of whether or not the state diagram remains equivalent).

    Please note: The question is marked based on how well you follow the steps of the algorithm of section 9.1.¹

2. (3 marks) Using the method described in Section 9.2 (and in videos of Week 3), convert the state diagram given in Figure 1 into an equivalent regular expression. Here Σ = {a, b, c, d}.

    Your answer should include the intermediate step(s) used in the construction.

    ¹An NFA produced by some other method is considered incorrect independently of whether or not it may define the same language.

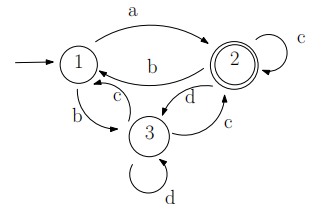
Figure 1: State diagram for Question 2.

3. Are the following languages A and B over the alphabet Σ = {a, b, c, d} regular or nonreg-ular?

• For a language that is regular, give a regular expression that defines it.

• For a nonregular language, using the pumping lemma prove that it is not regular.

(a) (2 marks)

(b) (2 marks)

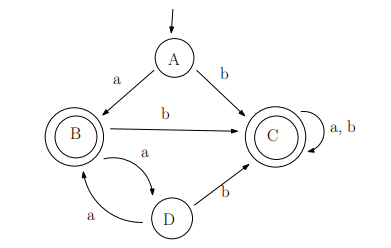
4. (3 marks) Using the algorithm mark distinguishable pairs of states that is presented in Week 4 videos 22–24 (and can be found in the course notes), minimize the number of states of the DFA depicted in Figure 2.

    Your answer should indicate in detail how you arrived at the solution:

• For each stage of the algorithm, indicate which pair(s) of states are marked as distinguishable and explain the reason why.

• Draw the minimized state diagram where each state is labeled by the corresponding names of states in the original DFA that were merged together.

5. (6 marks) Let Σ = {a, b, c, d}. Give context-free grammars that generate the following languages. In each case, also give a derivation of the specified terminal string using your grammar. The derivation beginning from the start variable should indicate each individual derivation step using the notation ⇒.