International baccalaureate diploma

Mathematics

 

 

Mathematical extended essay

 

 

Research question: To investigate the relationship between the angle of intersection of a circular cone and major-minor axes and what are the different ways to obtain the ellipse with the largest area by cutting a cone with a fixed volume?

 

Word count:

Contents:

Chapter 1: Introduction

1.1. Background information…………………..…………4

1.2. The circular cone………………………....……………5

1.3. The conic section…………………....…………………7

1.4. The ellipse………………………………….....…………8

1.5. The major-minor axes…………….………………….9

Chapter 2: Methodology…………………...…………………10

Chapter 3: Analysis……………………………….....…………11

Chapter 4: Evaluation and discussion………..………....14

Chapter 5: Conclusion…...……………………….....……….15

Chapter 6: Bibliography…………………………....…………16

Background information:

There are parabola, ellipse, hyperbola, regular triangle and regular circle in conic section. The cross section is parabola, parallel to the cone a prime line cut can be obtained; the cross section is ellipse, inclined to the cone axis cut can be obtained; the cross section is hyperbola, parallel to the cone axis cut can be obtained; the cross section is regular triangle, through the cone top, perpendicular to the cone axis cut can be obtained; the cross section is regular circle, parallel to the cone bottom cut can be obtained.

The optical properties of conic are widely used in the field of lighting and energy. For example, the searchlight is often designed as a paraboloid, and the light source is set at the focus to get the parallel light, which effectively reduces the divergence of light. Another example is a solar cooker, which in turn receives parallel light and puts the object to be heated in focus. Similarly, the "big pot cover" of TV antenna also uses this conic optical property to enhance the signal.

 

The conic cone

A cone is a geometric figure, which has two definitions. Definition of analytic geometry: the spatial geometric figure composed of a conical surface and a plane that cuts it (satisfying that the intersection line is a circle) is called a cone. Solid geometry definition: take the straight line of the right side of the right triangle as the axis of rotation, and the other two sides rotate 360 degrees to form a curved surface, which is called a cone. The axis of rotation is called the axis of a cone. The surface formed by the rotation of the edge perpendicular to the axis is called the base of the cone. The side of a cone is a curved surface formed by rotating an edge that is not perpendicular to the axis. No matter where the rotation is, the side that is not perpendicular to the axis is called the generatrix of the cone.

There are some properties of conic cone, I am going to use in the internal assessment, which is:

The height of a cone: the shortest distance between the apex of a cone and the center of the bottom of a cone is called the height of a cone.

Cone generatrix: the radius of the sector formed by the expansion of the side of the cone, and the distance from any point on the circumference of the bottom surface to the vertex.

The side area of a cone: the side of the cone is expanded along the generatrix, which is a sector. The arc length of the sector is equal to the perimeter of the bottom of the cone, and the radius of the sector is equal to the length of the generatrix of the cone. The side area of a cone is that the arc length is the perimeter of the bottom of the cone x eneratrix/2; when it is not expanded, it is a curved surface.

A cone has a bottom, a side, a vertex, a height, and numerous generatrix. The expanded view of the bottom is a circle, and the expanded view of the side is a fan.

The conic section

In mathematics, a conic section (or simply conic) is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse. In this internal assessment, one rule I’m going to apply is that when the plane intersects only one side of the conic, and there is no conic vertex, the result is ellipse.

 

The ellipse

An ellipse is a curve in a plane around two focal points, so that for each point on the curve, the sum of the distances to the two focal points is constant. Therefore, it is a generalization of circle, which is a special type of ellipse with two focal points at the same position. The shape of an ellipse is represented by its eccentricity. For an ellipse, it can be any number from 0 to any number close to but less than 1.

An ellipse is a closed cone section: a plane curve intersected by a cone and a plane. There are many similarities between ellipse and other two forms of cone section: parabola and hyperbola, both of which are open and unbounded. The cross section of the cylinder is elliptical unless it is parallel to the axis of the cylinder.

An ellipse can also be defined as a set of points such that the ratio of the distance of each point on the curve to the distance of a given point (called the focus) to the distance of the same point on the curve which is directrix is a constant. This ratio is called the eccentricity of the ellipse.

 

The major-minor axes

In plane the distance of two fixed points between 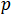 and 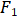 ,   equals to the constant 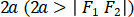 which is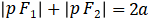 

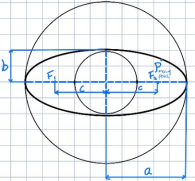
The two fixed points 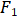,  are called the focal points of the ellipse, and the distance between the two focal points  is called the focal length of the ellipse.  is the moving point of the ellipse.

The chord of the line where the ellipse section coincides with the line connecting the two focal points is the major axis and 

the length is .

The chord is the minor axis, and the length is .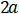

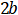Methodology:

Let xP , yP , zP denote the Cartesian coordinates of a point P. Suppose P and Q are two distinct points. The length of line segment P Q is denoted by l(P Q), and the gradient of P Q is denoted by g(P Q) which is defined as g(P Q) = |zQ − zP | q (xQ − xP ) 2 + (yQ − yP ) 2 .

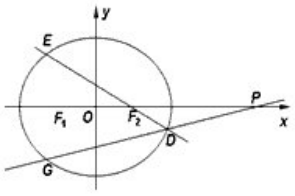
(1) Let C(P; m) denote a (double-napped) right circular cone whose vertex is P and whose generating lines have gradient m (m > 0). The angle β formed by the axis of C(P; m) and the generating lines is referred to as the generating angle of the cone. Clearly, tan β = 1/m.

Now suppose A and B are two distinct points in space. The intersection of cones C(A; m) and C(B; m) is denoted by C(A, B; m). Assume the horizontal distance between A and B is 2u while the vertical distance between A and B is 2h. Then, after a transformation we may assume A = (u, 0, h), B = (−u, 0, −h), u ≥ 0, h ≥ 0 (Fig. 1). Hence the equations describing C(A; m) and C(B; m) are (x − u) 2 + y 2 = (z − h) 2 m2 , (x + u) 2 + y 2 = (z + h) 2 m2 .

 

 (2) If h = 0, then the intersection C(A, B; m) lies trivially in the Y Z-plane. Assume h 6= 0. Subtracting the first equation from the second, we have z = m2 u h x = m2 k x, where k = h/u = g(AB). It follows that C(A, B; m) lies on a plane P˜ which contains the Y -axis and meets the XY -plane at an angle α, referred to as the intersecting angle of two cones. We call this planar curve C(A, B; m) a conic section, or simply a conic. In particular, if g(AB) ≥ m, C(A, B; m) is a closed curve and called an ellipse (Fig. 1(1)); if g(AB) ≤ m, C(A, B; m) has two separate branches, called a hyperbola (Fig. 1(2)). Trivially, in their degenerate cases in which g(AB) = m, an ellipse becomes a line segment AB, and a hyperbola becomes two half-lines that are the extensions of AB. Moreover, there are two special cases: 1. If A, B lie in a vertical line, then g(AB) = ∞ and the ellipse is a circle lying in a horizontal plane. 2. If A, B lie in a horizontal plane, then g(AB) = 0 and the hyperbola lies in a vertical plane. Substituting z with the right side of (3), from (2) we obtain y = ± p (m2u 2 − h 2)(m2x 2 − h 2) mh .

(4) Hence the parametric expression of C(A, B; m) is à x, ± p (m2u 2 − h 2)(m2x 2 − h 2) mh , m2u h x ! . (5) Let VA and VB be the intersections of C(A, B; m) with the XZ-plane that are close to A and B respectively (Fig. 1).

 

 Then by Equations (3) and (4) VA = ( h m , 0, mu), VB = (− h m , 0, −mu). Clearly, C(A, B; m) is symmetric with respect to two orthogonal lines: VAVB and the Y -axis. Therefore, O is the center of the conic section C(A, B; m). When C(A, B; m) is an ellipse, let R1 and R2 be the intersections of C(A, B; m) with the positive and negative Y -axis respectively. Then again from Equation (4) we find R1 = µ 0, u m q |k 2 − m2|, 0 ¶ , R2 = µ 0, −u m q |k 2 − m2|, 0 ¶ .

 

(7) When C(A, B; m) is a hyperbola, (also defines two points on the Y -axis. In the case of an ellipse, VAVB is called the major axis while R1R2 is called the minor axis of the ellipse. In the case of a hyperbola, VAVB is called the transverse axis while R1R2 is called the conjugate axis of the hyperbola. From Equations (4) and (3), it is easy to derive that y 0 x = ±(m2 /k2 − 1)x/y, z0 x = m2 /k. Therefore, the tangent vector t of the conic section C(A, B; m) is t = Ã 1, ±( m2 k 2 − 1)x y , m2 k ! .

 

(8) Remark 1 Note t is completely determined by m and k, independent from the coordinates of A and B. Now suppose C(A, B; m) is a hyperbola. When x goes to infinity, by (4) y/x goes to p m2/k2 − 1 and the tangent vector becomes t∞ =  0, ± s m2 k 2 − 1, m2 k.

 

Analysis:

The two lines through O in the directions of t∞ are the asymptotes of the hyperbola, which lie in the plane P˜ where the hyperbola lies. Conic sections have two important properties: constant sum/difference property and reflective property.

First we prove a lemma [5]. Lemma 2 Suppose the endpoint S of a line SA is perturbed in direction v. Let the angle between −→SA and v be θ. Then the directional derivative of l(SA) with respect to v is (− cos θ). Proof: Suppose S moves to S ∗ in direction v. Let l0 = l(SA), l = l(S ∗A), ε = l(SS∗ ). Then l 2 = l 2 0 + ε 2 − 2εl0 cos θ, and 2l · dl = 2(ε − l0 cos θ) · dε. Note l → l0 when ² → 0. Therefore l 0 v = limε→0 dl dε = − cos θ. The lemma is proved.

Theorem 3 (constant sum/difference) For any point S on an ellipse C(A, B; m), the sum of the distances from S to the vertices A and B is constant. For any point S on a hyperbola C(A, B; m), the difference of the distances from S to the vertices A and B is constant. Proof: There is no loss of generality that we assume A = (u, 0, h), B = (−u, 0, −h) as before. Because g(AS) = g(BS) = m, when k ≥ m and C(A, B; m) is an ellipse, l(AS) + l(SB) = p 1 + m−2(|ZA − ZS| + |ZS − ZB|) = 2h p 1 + m−2. The argument is similar for the case of C(A, B; m) being a hyperbola.

This property completely characterizes ellipses and hyperbolas, therefore, we can redefine ellipses/hyperbolas to be planar curves that satisfy the constant sum/difference property. That is, an ellipse (or a hyperbola) is a planar curve such that the sum (or difference respectively) of the distances between any point on the curve and two fixed distinct points is constant.

This property implies another property which is important in applications of conic sections. Corollary 4 (reflection) For any point S on an ellipse or a hyperbola, the tangent line at S meets SA and SB at the same acute angle. Proof: Let the acute angle between t and SA, SB be θ, φ respectively. By Lemma 2, l 0 t (SA) = − cos θ, l0 t (SB) = − cos(π − φ) = cos φ.

For an ellipse, since l(SA) + l(SB) is constant, l 0 t (SA) + l 0 t (SB) = − cos θ + cos φ = 0. Hence θ = φ.

The argument is similar for hyperbolas. Remark 5 This corollary can also be proved by Equation (8). Because of the reflective property A and B are called the inherent foci of C(A, B; m). Let A, ¯ B¯ and ¯C(A, ¯ B¯) be the projections of A, B and C(A, B; m) on a horizontal plane respectively. Then any point S¯ on ¯C(A, ¯ B¯) is the projection of certain point S on C(A, B; m). Because l(A¯S¯) ± l(S¯B¯) = (l(AS) ± l(SB)) sin β = const, ¯C(A, ¯ B¯) is also an ellipse or a hyperbola with foci A¯ and B¯. Since A¯ and B¯ lie on the same plane where the curve ¯C(A, ¯ B¯) lies, we call them coplanar foci of the curve. Moreover, let V¯A, V¯B, R¯ 1 and R¯ 2 be the projections of VA, VB, R1 and R2 on the same plane respectively. Then V¯AV¯B and R¯ 1R¯ 2 are the major and minor axes (or the transverse and conjugate axes) of the ellipse (or the hyperbola respectively) ¯C(A, ¯ B¯).

The equation of ¯C(A, ¯ B¯) can be easily derived from Equation (4) as follows: x 2 a¯ 2 + y 2 ¯b 2 = 1, (9) where a¯ 2 = h 2 m2 , ¯b 2 = h 2 − m2u 2 m2 = (k 2 − m2 )u 2 m2 . (10) Equation (9) is called the standard form of an ellipse or a hyperbola, depending on ¯b 2 ≥ 0 or ¯b 2 ≤ 0, i.e. on k ≥ m or k ≤ m. Note that 2¯a = l(V¯AV¯B), 2 ¯b = l(R¯ 1R¯ 2). Let 2¯c = l(A¯B¯) = 2u. Then it is easy to see that c¯ 2 = ¯a 2 − ¯b 2 , if ¯C(A, ¯ B¯) is an ellipse, c¯ 2 = ¯b 2 − a¯ 2 , if ¯C(A, ¯ B¯) is a hyperbola.

The shape of a conic section is completely determined by two parameters m and k. Now we investigate how the curve varies as m or k changes. (1) If A and B are fixed, i.e. k is fixed, but m changes, we obtain a family of conics that lie on different planes but share A, B as their common foci. These conics are called confocal. As argued above, when these curves are projected to the same horizontal plane, their projections are also confocal with A, ¯ B¯ as their common foci (Fig. 2, based on a figure in [3]). (2) Now we study how C(A, B; m) varies if m is fixed but k changes. Without loss of generality we assume B is fixed and A moves to A∗ that lies in the same vertical plane. Let A∗ = (u+ε, 0, h+ δ), ε ≥ 0, δ ≥ 0. Then the equations of cones C(A∗ ; m) and C(B; m) become (x − u − ε) 2 + y 2 = (z − h − δ) 2 m2 , (x + u) 2 + y 2 = (z + h) 2 m2 . (11) Of all possible moves of A we discuss the moves in three special directions: along BA, horizontal and along VBA. (2.1) A move of A either preserves the gradient between two cone vertices or does not. If it does, then δ/ε = h/u = k. Solving the system (11) with δ = kε we have z = m2 k x + (h 2 − m2u 2 )ε 2hu . Therefore, the new conic section C(A∗ , B; m) lies in a plane P ∗ that is parallel to the plane P˜ where C(A, B; m) lies.

 Besides, since both curves lie on the same cone C(B; m), it follows that the two conics C(A∗ , B; m) and C(A, B; m) are similar relative to their common focus B. When projected on the same horizontal plane, their projections are also similar relative to B¯  On the other hand, if the move of A does not preserve the gradient between the vertices, then P ∗ is not parallel to P˜ , and C(A∗ , B; m) is not similar to C(A, B; m) by the definition of similarity. 6 A curve C1(x1(t), y1(t), z1(t)) is said to be similar to another curve C2(x2(t), y2(t), z2(t)) relative to point (x0, y0, z0) if x2(t) − x0 x1(t) − x0 = y2(t) − y0 y1(t) − y0 = z2(t) − z0 z1(t) − z0 . (2.2) The vertex A moves in the direction of the positive X-axis, that is, δ = 0 and ε monotone increases.

Evaluation and discussion

 For this reason, B is called the inherent focus of the hyperbola, and L is called the directrix associated with the inherent focus B. As ellipses and hyperbolas, this equidistance property completely characterizes parabolas and we can redefine a parabola to be a planar curve that satisfies the equidistance property. The ratio of the distance from S to the focus to the distance from S to the directrix is called the eccentricity of the parabola. Thus, a parabola can also be defined as a planar curve whose eccentricity is one. Again, the equidistance property implies the reflective property: Corollary 8 (reflection of parabolas) For any point S on a parabola, the tangent line t at S meets two lines at the same acute angle: the line joining S and the focus and the perpendicular from S to the directrix. Now denote the parabola by C(B, L; m). Let ¯C(B, ¯ L¯), V¯B, B, ¯ S, ¯ L¯ and D¯ be the projections of C(B, L; m), VB, B, S, L and D on a horizontal plane respectively. Because SB and SD have the same gradient, l(SB) = l(SD) implies l(S¯B¯) = l(S¯D¯). Therefore, the projection ¯C(B, ¯ L¯) is also a parabola, whose coplanar focus is B¯ and the directrix associated with B¯ is L¯. From (12) the equation of ¯C(B, ¯ L¯) is y 2 = 4¯p(x + h/m), where ¯p = h/m − u is the distance from the vertex V¯B to the coplanar focus B¯ or to the directrix L¯. This equation is the standard form of a parabola with vertex at (−h/m, 0). If the origin moves to the vertex V¯B, then the equation is further simplified to y 2 = 4px.

Conclusion:

Assume we start with g(AB) = k > m and the conic is an ellipse. In this move, the ellipse C(A, B; m) becomes narrower and narrower, and finally becomes a line segment, a degenerate ellipse with k ∗ = (h+δ)/(u+ε) = m. If the increase of ε continues, then as stated in Section 2, the line segment first suddenly jumps into two half-lines as a degenerate hyperbola, and then becomes a normal hyperbola with k ∗ < m. (2.3) As we have discussed in (2.2), in the degenerate case, an ellipse or a hyperbola overlaps the line through A and B. One may ask if there is a non-degenerate common extreme of ellipses and hyperbolas. Look at the move of A along VBA. In such a move δ = mε. Solving the system (11) with δ = mε and then let ε go to infinity, we have y = ± 2 p (h − mu)(mx + h) m , z = m(x − u) + h. (12) Therefore the parametric expression of the resulting curve is à x, ± 2 p (h − mu)(mx + h) m , m(x − u) + h ! . If starting with a hyperbola (h/k < m), we obtain the same result. Therefore, the resulting planar curve, called a parabola, is the non-degenerate common extreme of ellipses and hyperbolas. The parabola has a vertex VB and is symmetric about the line VBA∗ , the intersection of P˜ and the XZ-plane. Let L = {(− 2h m + u, y, −h)} be the point set that is the intersection of the plane P˜ and the horizontal plane through B (Fig. 3). For any point S on the parabola, let D be the foot of the perpendicular from S to L. Then the gradient of SD is the slope of the plane P˜ , which is equal to the gradient of any generating line of C(B; m). Therefore, similarly to the argument for ellipses and hyperbolas, we have l(SB) = l(SD). Theorem 7 (equidistance) For any point S on the parabola, the distance from S to B equals the distance from S to the line L.

Bibiliography:

1. Kanas, S. , & Wiśniowska, A. (1998). Conic regions k-uniform convexity, ii. oficyna wydawnicza politechniki rzeszowskiej.

2. Bookstein, F. L. . (1979). Fitting conic sections to scattered data. Computer Graphics and Image Processing, 9(1), 56-71.

3. Zimmermann, T. , Premraj, R. , & Zeller, A. . (2007). Predicting Defects for Eclipse. International Workshop on Predictor Models in Software Engineering. IEEE.

4. Zimmermann, T. , Premraj, R. , & Zeller, A. . (2007). Predicting Defects for Eclipse. (pp.9-9).

5. Georghiades, A. S. , Belhumeur, P. N. , & Kriegman, D. J. . (2002). From few to many: illumination cone models for face recognition under variable lighting and pose. IEEE Transactions on Pattern Analysis & Machine Intelligence, 23(6), 643-660.

6. Georghiades, Athinodoros, S., Belhumeur, Peter, & N., et al. (2001). From few to many: illumination cone models for face recognition under variable lighting and pose. IEEE Transactions on Pattern Analysis & Machine Intelligence.