CSC165H1: Problem Set 1

Due Tuesday 2 February before 17:00

General instructions

Please read the following instructions carefully before starting the problem set. They contain important information about general problem set expectations, problem set submission instructions, and reminders of course policies.

      • Your problem sets are graded on both correctness and clarity of communication. Solutions that are technically correct but poorly written will not receive full marks. Please read over your solutions carefully before submitting them.

      • Each problem set may be completed in groups of up to three—except for Problem Set 0. If you are working in a group for this problem set, please consult https://github.com/MarkUsProject/Markus/wiki/Student-Guide for a brief explanation of how to create a group on MarkUs.

      • Solutions must be typeset electronically, and submitted as a PDF with the correct filename. Hand-written submissions will receive a grade of ZERO.

The required filename for this problem set is problem set1.pdf.

      • Problem sets must be submitted online through MarkUs. If you haven’t used MarkUs before, give yourself plenty of time to figure it out, and ask for help if you need it! If you are working with one or more partner(s), you must form a group on MarkUs, and make one submission per group. “I didn’t know how to use MarkUs” is not a valid excuse for submitting late work.

      • Your submitted file(s) should not be larger than 9MB. You might exceed this limit if you use a word processor like Microsoft Word to create a PDF; in that case, you should look into PDF compression tools to make your PDF smaller, although please make sure that your PDF is still legible before submitting!

      • Submissions must be made before the due date on MarkUs. Please see the Assessment section on the course website for details on how late submissions will be handled.

      • MarkUs is known to be slow when many students try to submit right before a deadline. Aim to submit your work at least one hour before the deadline. It is your responsibility to submit your work ahead of time to meet the deadline. You can submit your work more than once; the most recent version submitted within the deadline (or within the late submission period) is the version that will be marked.

      • The work you submit must be that of your group; you may not use or copy from the work of other groups, or external sources like websites or textbooks. Please see the section on Academic Integrity in the course syllabus for further details.

Additional instructions

      • You may not define your own propositional operators, predicates, or sets for this problem set, unless the question asks for it explicitly. Please work with the ones we have introduced in lecture, and any additional definitions provided in the questions themselves.

      • Final expressions in predicate logic must have negation symbols (¬) applied only to predicates or propositional variables, e.g., ¬p or ¬Prime(x). To express “a is not equal to b,” you can write a  b.

      • Please review the section Our conventions for writing formulas on pp. 29–31 of the Course Notes, and in particular the precedence rules for the different operators and quantifiers.

1. [10 marks] Translating statements.   Trees can be grouped into forests. Some trees are pine trees, and some trees are oak trees (in this question, these are the only kinds of trees we will consider). Here are some sets and predicates to model trees and forests.

Warning!   In this question, the symbols T and F represent sets. If you need to denote truth values, please use the full names True and False in order to avoid any confusion!

Using these sets and predicates, the symbols = and , set notation (∩, ∪, ⊆, ∈, etc.), and the standard propositional operators and quantifiers from lecture, translate each of the following English statements into predicate logic.

   (a) There is exactly one tree that is not in a forest.

   (b) There is a forest of oak trees.

   (c) All pine trees are in the same forest.

   (d) No forest contains both pine and oak trees.

   (e) Every group of trees is a forest.

2. [4 marks] Venn diagrams.   Sets can be represented by Venn diagrams. These are overlapping circles, with the different regions formed representing the result of different set operations. For example, the set A ∩ B is show below by the region shaded in grey:

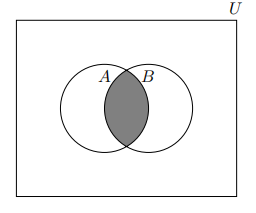
(a) Write an expression representing the set shown in grey in the following diagram:

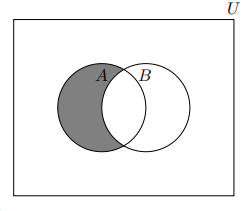
(b) Draw a Venn diagram representing the set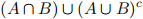 

(c) Write an expression representing the set shown in grey in the following diagram:

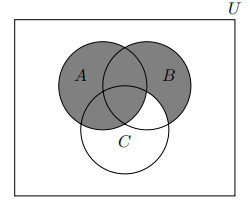
(d) Draw a Venn diagram representing the set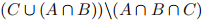 

3. [8 marks] Choosing sets and predicates—Updated at 08:45 on Tuesday 26 January. This question gets you to investigate some of the subtleties of variable scope and precedence rules that are discussed on pp. 29–31 in the Course Notes.

Consider the following statements:

∀x ∈ S, ∃y ∈ T,(P(x) ∨ Q(x, y)) ∧ (¬P(x) ∨ ¬Q(x, y))

∃y ∈ T, ∀x ∈ S,(P(x) ∨ Q(x, y)) ∧ (¬P(x) ∨ ¬Q(x, y))

(a) Provide one definition of sets S and T, and predicates P and Q, that makes the first statement true and the second statement false. Your sets must be non-empty, and your predicates may not be constant functions (i.e., always True or always False). Briefly justify your response, but no formal proofs are necessary.

(b) Is it possible to provide one definition of sets S and T, and predicates P and Q, that makes the first statement false and the second statement true? Your sets must be non-empty, and your predicates may not be constant functions (i.e., always True or always False).

If it is possible, describe the sets and briefly justify your response; if not, give a brief explanation as to why it is not possible. No formal proofs are necessary.

4. [13 marks] Working with infinity.   Sometimes when dealing with predicates over N, we don’t care so much about which numbers satisfy the given predicate, or even exactly how many numbers satisfy it. Instead, we care about whether the predicate is satisfified by infinitely many numbers. For example:

“There are infinitely many even numbers.”

One way we can express the idea of “infinitely many” is by saying that for every natural number n0, there is a number greater than n0 that satisfies a predicate. For example:

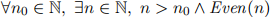
You may use the Even and | (“divides”) predicates in your solutions for all parts of this question.

(a) Express the following statement in predicate logic: “There are finitely many odd natural numbers.”

(b) We might want to say something stronger about even natural numbers. In particular, given one even number, we now how to find infinitely many other even numbers.

Express the following statement in predicate logic: “Zero is an even number, and given any even number, two more than that number is also an even number.”

(c) Consider the following definition.

Definition 1. Let a ∈ N. We say that a is a perfect number when it is equal to the sum of all of its divisors, excluding itself. For example, 6 is a perfect number since 6 = 1 + 2 + 3.

Translate the following statement into predicate logic: “There are infinitely many even perfect numbers.”

You may not define your own predicate for “Perfect” in this part. Here, we’re looking for you to translate the above definition and embed that translation into a larger logical statement. You may use the indicator function, I(p), which is equal to 1 when p is true, and 0 when p is false, for any proposition p. For example, you could write the sum of the first 100 even natural numbers as:

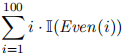
(d) Here is another variation of combining predicates with infinity. Let P : N → {True, False}. We say that P is eventually true when there exists a natural number n0 such that all natural numbers greater than n0 satisfy P.

Use this idea to express the following statement in predicate logic (no justification is required here):

Eventually, all perfect numbers are odd.