0    Instructions

The LaTeX source for this file is provided as a template for the assignment. Copy it into a new .tex file or Overleaf. Make sure that homework.cls is in the same directory - it provides many useful packages and commands we will use throughout the quarter, and is needed to compile.

Type your answers below each part of each problem.

Leave a blank line to start a new paragraph or use \bigbreak for extra space.

1   Asymptotic Runtime (7 points)

For each of the following code snippets, compute (with explanation) the asymptotic running time of the algorithm.

•   Algorithm 1 ArrayDelete(A[1..n])

     Require: A[1..n] is an array of numbers

     1: for i = 1..n do

     2:    delete A[0]

     3: end for

•   Algorithm 2 PrintMins2D(A[1..n])

     Require: A[1..n][1..m] is a 2D-array of numbers

     1: for i = 1..n do

     2:    mn ← minj (A[i][j])

     3:    print(mn)

     4: end for

•   Algorithm 3 FindMin1(A[1..n])

     Require: A[1..n] is an array of numbers

     1: if n == 0 then

     2:    return ∞

     3: else if n == 1 then

     4:    return A[1]

     5: else

     6:    mid ← bn/2c

     7:    return min(FindMin1(A[1..mid]), FindMin1(A[mid + 1..n]))

     8: end if

•   Algorithm 4 FindMin2(A[1..n])

     Require: A[1..n] is an array of numbers

     1: if n == 0 then

     2:    return ∞

     3: else

     4:    return min(A[1], FindMin2(A[2..n]))

     5: end if

•   Algorithm 5 SumToN1(n)

     Require: n is a non negative integer

     1: if n == 0 then

     2:    return 0

     3: else

     4:    return n + SumToN1(n - 1)

     5: end if

•   Algorithm 6 SumToN2(n)

     Require: n is a non negative integer

     1: sum ← 0

     2: for i = 0..n do

     3:    for j = 0..i do

     4:       sum ← sum + 1

     5:    end for

     6: end for

     7: return sum

•   Algorithm 7 A(n)

     Require: n is a non negative integer

     1: for limit = 1 to n do

     2:    current = 5

     3:    while current < limit do

     4:       current ← current ∗ 7

     5:    end while

     6: end for

2    Three-way Mergesort (10 points)

Consider the following mergesort variant: instead of dividing a list of n elements into two halves, we divide it into three thirds of approximately equal size. Then we recursively sort each third and merge the three lists by comparing their respective first elements and taking the smallest.

•  (3 points) Write pseudocode for a 3-way merge procedure that takes as input three sorted lists each of size n/3. (You may assume n is a power of 3.) Pay careful attention to the formulas for interval endpoints. Your algorithm should run in O(n) time.

•  (3 points) Prove that your algorithm is correct. (See CLRS correctness proof for Merge on pages 32–34.) Simply restating the steps of the algorithm will receive no credit.

•  (1 point) Write pseudocode for a 3-way mergesort algorithm. Use your 3-way merge procedure as a subroutine.

•  (1 point) Let T(n) denote the running time of 3-way mergesort on an array of size n. Write a recurrence for T(n) and solve it using the master theorem.

•  (1 point) Is 3-way mergesort asymptotically faster than insertion sort? Prove your answer. (Hint: Take the limit of the ratio of the running times as n → ∞)

•  (1 point) Is 3-way mergesort asymptotically faster than standard mergesort? Prove your answer. (See previous hint.)

3    Finding Alice (15 points)

Alice got lost in a park and our goal is to find her quick. A park is represented by a m-by-n grid P[1..m][1..n]. What we know is that Alice never revisited the same square, and at each square we know which direction Alice exited.

Figure 1 shows an example of the problem instance.

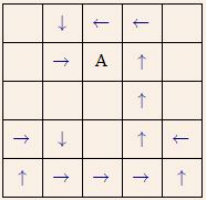
Figure 1: Q3 example.

You can assume that each entry of P is either ”up”, ”down”, ”left”, ”right”, ”A” or blank. Alice starts at P[1][1] (i.e. the bottom left corner in the diagram above) and never leaves the boundary (e.g., when she was at the top row, she did not go up). The goal is to determine which entry of P entry contains ”A”.

(a)  (1 point) Consider the algorithm that simply follows Alice’s trail. What is the worst-case running time of this algorithm? Give an example for the worst-case instance.

(b)  Consider the case that m = 1, i.e., the park is a path of length n. Alice started at the leftmost square and can only go right (since she did not revisit the same square and cannot go outside of the boundary).

(3 points) Give an algorithm that finds Alice in O(log n) time. Write pseudocode for your algorithm.

(c)  Consider the general case where both m and n can be greater than one.

i.  (6 points) Give an O(m + n) time algorithm for finding Alice. Write pseudocode or describe each step of your algorithm clearly in English.

ii.  (3 points) Prove that your algorithm is correct.

iii.  (2 points) Analyze the worst-case running time of your algorithm.

4    Programming: Local Minima (15 points)

Throughout the quarter, we will use GitHub Classroom for programming assignments.

•  (15 points) Please complete the HW1 programming assignment, which involves fifinding local minima in 1D and 2D arrays. Follow the link to accept the assignment and read the README for instructions.