Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Physics 460 - Homework 3 - Winter 2022

We consider an electron in a one-dimensional potential of the form

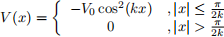
Here, V0 = 1EH (one Hartree), with the atomic energy unit, EH = α2m0c2 , with electron rest mass m0 and fine structure constant α. See https://en.wikipedia.org/wiki/Hartree atomic units . Practically, EH ≈ 27.2 eV is good enough to check equations. Also, in this problem k = 0.05/a0, with Bohr radius a0. Using the methods discussed in class and posted on Canvas, find the bound-state energies up to n = 20 and normalized wave functions up to n = 5. For numerical integration, use the Numerov method. https://en.wikipedia.org/wiki/Numerov%27s method

Your submission should have the following sections:

Section 1: (10 pts) A brief table and description that shows critical parameters of the computation. This includes a statement about the machine precision you are using (that may be 4, 8 or 16-byte real), the energy limits in units EH, the energy step size ∆E in your level search in units EH, the spatial step size ∆x in units a0, and your integration limits ±xmax in units a0, and an estimate of the final uncertainty δE of your energy levels in units EH. You may estimate your energy uncertainties δE from the stability of your numerical results against variation of step size parameters. We will check the deviation of your energy values from nominal energy values (that we have), and compare the defects against your claimed uncertainties δE. All energy quantities must be expressed in units of EH, and length quantities in units of a0. You may include detailed discussions of your methods as you see fit.

Section 2: (10 pts) A list of your energy values relative to the potential minimum, En +V0, in units of EH. Label them as follows: n = 0 is for the ground state, 1 is for the first excited state, and so on. If you find more than 21 states, limit your data table to n ≤ 20. Discuss as needed. It may, for instance, be the case that your uncertainty δE and / or xmax are state-dependent.

Section 3: (10 pts) A set of plots of the SQUARES of your normalized wave-function-magnitudes vs x. If you find more than 5 states, limit your plots to n ≤ 5. Make sure to label all axes with numbers and units. The position axis must be in units a0. The wave-function density must have the unit 1/a0. All labels and writing MUST be legible without forcing the reader to resort to using magnifying glasses. Plots must be neatly organized. Presentation quality WILL be considered in the grading.

Section 4: (20 pts) A source code listing in Python, C, Fortran or else. Please google “Source code listing” for the exact meaning of this term. Provide a source code file that compiles on a generic system, with no optional math packages installed. Your listings will be carefully examined according to the following rules: 1. Code must be self-contained. 2. Shells that simply call canned routines that do the bulk of the work in a black box are not allowed and will carry only minimal score or no score (depending on case). 3. Along the same lines, canned “differential-equation solvers” are not allowed. You must not call any subroutines that you did not write yourself. 4. The use of self-written subroutines is encouraged. These must be included in your source code listing.

Template:

Section 1

Machine precision in bytes:

Energy search range in EH: From ..... to ....., in steps of ∆E =....

Typical energy uncertainty of obtained levels in EH: δE = .....

Spatial integration range and step size in a0: xmax =....., in steps of ∆x =.....

Discussion: up to one page.

Section 2