Chem113b - Homework assignment 3 2022
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Chem113b - Homework assignment 3
2022
(I) We will inspect the time evolution of an expectation value of an operator Oˆ . Consider the expectation value of Oˆ for quantum state represented by the wavefunction Φ(x):
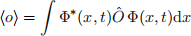
We denote the expectation value by angle brackets, i.e., ⟨···⟩. Use the time-dependent Schr¨odinger equation:
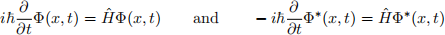
where the second identity stems from the self-adjointness (i.e., “Hermicity”) of the Hamil- tonian operator. Prove that the following identity holds for an expectation value ⟨o⟩ of an operator Oˆ :
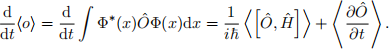
where hOˆ , Hˆi is the commutator of Oˆ and Hˆ. To prove this, consider taking the time
derivative of the expectation value integral with wavefunction of an arbitrary quantum state Φ(x). Note: the partial derivative means we consider the explicit dependence of Oˆ on time – we have not encountered such operators in practice.
(II) Consider two functions:
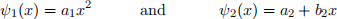
The two functions should represent some (arguably weird) wavefunction of a “quantum” particle which is confined to the domain x ∈ [ − 1 : 1]. Find the constants a1,a2,b2 so that simultaneously: (i) the wavefunctions are appropriately normalized and (ii) the two wavefunctions are orthonormal on the domain, i.e,
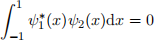
Hint: To obtain the coefficients, first normalize ψ1(x), ensure that ψ1(x) and ψ2(x) are orthogonal, and then normalize ψ2(x).
(III) Consider a particle in an infinite 1D potential well with width L, which is positioned sym- metrically around zero ( − 
≤ x ≤ 
). The eigenstates solved from time-independent Schr¨odinger equation read below:
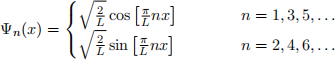
Use the position operator 
and momentum operator pˆ to calculate the position ⟨x⟩ and momentum ⟨p⟩ for the third lowest energy state.
(IV) Consider a superposition ψ+(x,t) of a particle in an infinite 1D unit well, which is positioned symmetrically around zero ( − 
≤ x ≤ 
). Assume the superposition ψ+(x) is equally composed by the ground state and first excited state at time t = 0,
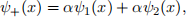
where α are real positive numbers that guarantee the proper normalization and enforce that ψ+(x) has indeed equal contributions of both ψ1(x) and ψ2(x). (Hint: see the lec- ture!) What’s the expectation value of 
at t = 0? With the time evolution operator, the superposition evolves dependent on time,
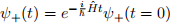
Note that the Hamiltonian in the exponent will act on an eigenstates ψ1 as: e − 
Hˆtψ1(x,t) = e − 
E1tψ1(x,t), where E1 is the energy ψ1. What will be the expectation value of position operator 
at t = 
ℏ1 , assuming E1 is the eigenenergy for the ground state?
(V) In class, we showed how we can approximate the behavior of simple conjugated polyenes by a 1D potential well. Let’s investigate the optical transition in hexatriene and octatetraene using this crude approximation. Assume that the carbon-carbon bond length is 1.4A˚ .
A Remember that each allowed electronic state is occupied by two electrons. Next find
the energies of the highest occupied and lowest unoccupied states, and compute the wavelength of the light that would be associated with a transition of an electron between those two.
B For 1,3-butadiene, we have shown in class that the energy matched pretty well: our
model prediction gave 6.0 eV, while the experiment gave 5.9 eV. The experimental data for hexatriene and octatetraene show that the maximum wavelength absorbed is 250 and 300 nm. Do these values agree with your results from the previous step? If not, why?
C How would the absorption of hexatriene and octatetraene change if we stretched the
molecule laterally by 10%?
(VI) Consider an electron in a 2D “nanoflake” (e.g., made out of graphene). We will approximate
the system by a 2D infinite potential well. We know, that the system is rectangular and we will approximate it as a square, i.e., Lx = Ly = L. Further, we know that it absorbs electromagnetic radiation with wavelength λ = 1379 nm (IR radiation). This is the largest wavelength absorbed by electrons, i.e., it corresponds to the excitation from lowest state to next higher energy state.
A How big is the nanoflake, i.e., what is its characteristic dimension L?
B If the “nanoflake” is strained along its y direction and therefore Ly is elongated by
5%. What will be the energy splitting of the two otherwise degenerate first excited states,i.e., the energy difference between the state of nx = 1,ny = 2 and the other state of nx = 2,ny = 1?
2022-02-08