Chem113b - Homework assignment 1 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Chem113b - Homework assignment 1
2021
(I) In photoemission experiment, one can estimate the work function Φ i.e., the minimum energy needed to remove an electron. Each incoming photon can knock-out a single electron and the total energy deposited on the sample is just the number of photons time the energy of the single photon. If the “quantum efficiency” of photoemission is 100% each photon knocks-out a single electron.
What is the maximum number of electrons that can be emitted if a magnesium surface with work function of 3.60 eV absorbs 8.36 × 10 −3 J of radiation at a wavelength of λ = 268 nm? What is the velocity, kinetic energy, and de Broglie wavelength of the electron emitted?
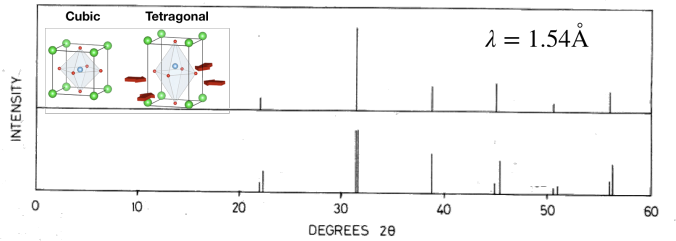
(II) BaTiO3 is a crystalline system that undergoes phase transition from cubic to tetragonal
symmetry; this means that its periodic arrangement of atoms in one case is the same in the x, y, and z directions (cubic phase) while in the transformed (tetragonal) phase only x and y directions are equivalent. The atoms form a periodic lattice with the spacing of dx = dy = dz = 4.031 A˚ for the cubic phase (i.e., the same spacing in all three directions). On the other hand, the spacing is dx = dy = 3.994A˚ and dz = 4.038A˚ for the tetragonal phase.
Compute at what lowest angle θ you will see a diffraction if you used x-rays with λ = 1.54 A˚; this is (arguably) the most common type of x-rays used in diffraction experiments. Note that diffraction will occur from the periodic arrangement of atoms along x, y, and z directions (characterized by spacings dx , dy, and dz) for each phase.
Below, you find x-ray diffraction plots (“difrractograms”) for the cubic and tetragonal crystal structures for BaTiO3. Due to the experimental setup, the diffraction pattern is collected as a function of double the diffraction angle, i.e., 2θ, where θ is the diffraction angle. The angles at which one observes the diffracted x-ray beam is clearly visible as intensity maxima. Which diffractogram corresponds to each of the crystalline phases? Explain Briefly your reasoning.
(III) The resolution of an optical microscope is roughly given by the wavelength of light – objects
with a size similar or smaller than the wavelength will diffract light, hence, we won’t be able![]() to clearly “observe” them. If we want to image individual atoms (which have a diameter of ∼ 1 A˚ = 10 − 10m), we need to use wavelengths that are much smaller than those of the visible light. In practice, we employ electron microscopy in which we exploit the wave- like properties of electrons. We “create” an electron beam by accelerating electrons in an electric potential. An electron accelerated by electric potential of 1V has kinetic energy 1 eV (see the previous example). What is the required accelerating potential in an electron microscope that produces electrons with wavelength λ = 0.25 A˚?
to clearly “observe” them. If we want to image individual atoms (which have a diameter of ∼ 1 A˚ = 10 − 10m), we need to use wavelengths that are much smaller than those of the visible light. In practice, we employ electron microscopy in which we exploit the wave- like properties of electrons. We “create” an electron beam by accelerating electrons in an electric potential. An electron accelerated by electric potential of 1V has kinetic energy 1 eV (see the previous example). What is the required accelerating potential in an electron microscope that produces electrons with wavelength λ = 0.25 A˚?
(IV) The diffraction of the monochromatic light on a grating creates multiple intensity maxima
on a screen. The distance between the grating and the screen is l = 3 m, and the slits in the grating are separated by g = 20 µm. The main maximum is located in the center of the screen, just opposite to the grating (i.e., at the diffraction angle θ = 0◦). Other maxima are observed on the sides of the main maximum. The first maximum (corresponding to θ ![]() 0◦ (i.e., on the side) is separated by a = 4.5 cm from the main maximum. What is the wavelength of the light?
0◦ (i.e., on the side) is separated by a = 4.5 cm from the main maximum. What is the wavelength of the light?
(V) We consider a double-slit experiment for electromagnetic waves, in which we observe the intensity of light on a screen, given by the expression:
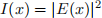
where E is the amplitude of the electromagnetic wave and x-coordinate represents the position on the screen. If slit 1 is closed, the amplitude of the electromagnetic wave on the
screen is:
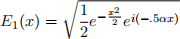
If slit 2 is closed, the amplitude of the electromagnetic wave on the screen is:
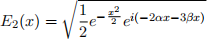
A) What is the intensity pattern on the screen, i.e., function I(x), if both slits are open? provide your result in form or real (exponential and a trigonometric) functions
B) Make a sketch of the probability density on the screen, I(x) (without using any potting tool, just draw an image by hand), and assume that both α and β are small numbers. Explain how will the resulting function look if if α and β increase.
(VI) Consider pairs wavefunctions on the domain x ∈ [−∞, ∞] (i.e., in the entire 1D space)

A) Analyze the orthogonality of ψ1 to all the remaining wavefunctions {ψj|j = 2, 3, 4} by computing the overlap integral R![]() ψ
ψ![]() (x)ψj(x)dx. Note that you do not need to com- pute all the integrals involved, because some of them will be zero due to the symmetry! (It is helpful if you sketch the functions by hand)
(x)ψj(x)dx. Note that you do not need to com- pute all the integrals involved, because some of them will be zero due to the symmetry! (It is helpful if you sketch the functions by hand)
B) What is the wavenumber and the wavelength of the quantum particle in state ψ4 if x is expressed in nm? Consider a slightly modified expression
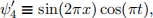
where t is the time argument in attoseconds. Does the state ψ![]() correspond to a standing wave? What is the period of oscillation of the state ψ
correspond to a standing wave? What is the period of oscillation of the state ψ![]() .
.
[Hint: the Gaussian integral is: 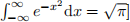
(VII) A standing wave is represented by a product of two periodic functions with only spatial and
only temporal dependence, i.e.,
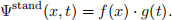
Consider a propagating wave described by the equation ψ1(x,t) ≡ Asin(kx −ωt). A standing
wave formed as a superposition of ψ1(x,t) and another (unknown) function ψ2(x,t), i.e.,
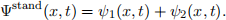
Note that the standing wave will be a superposition of two vibrations with the same wave number and frequency (otherwise you would not be able to separate spatial and temporal parts). Find ψ2(x,t) and the expression for Ψstand (x,t).
HINT: use the angle-sum identities of trigonometric functions sin and cos.
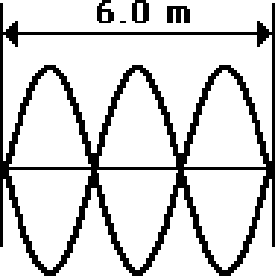
(VIII) The string below is 6.0 m long and is vibrating as the third harmonic shown in the graph
(The vibration amplitude is negligible compared to the string length). The string wave finishes 45 complete vibrational cycles in 10 seconds. Determine the frequency, period, wavelength and speed for this wave.
Use the following set of constants:
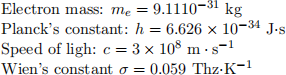
2022-02-08