AMATH 301 Rahman Coding Project 4
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
AMATH 301 RAHMAN
Coding Project 4
PRoBLEM 1
Consider the matrix equation
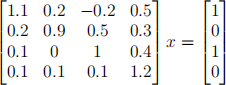
Implement the Jacobi algorithm as one function and Gauss-Seidel algorithm as another function to approx- imate the solution x.
INPUT: An ×n , bn ×1, and ∈ a positive real number.
OUTPUT: The smallest value of T such that the largest entry of the vector lAy - bl < ∈, and the actual
value of that entry, E = max lAy - bl.
STEP 1: Set y = zeros(n,1)
STEP 2: For T = 1, 2,... do STEP 3.
STEP 3: Update y according to Jacobi or Gauss-Seidel
STEP 4: Break when max lAy - bl < ∈
STEP 5: OUTPUT(T, E)
For Jacobi’s algorithm what is the smallest value of T such that the largest entry of the vector lAy - bl < ∈ for ∈ = 1e - 2 (recall this is just how we write 10-2 on MATLAB and Python)? Call this iteration Tj_2, and let Ej_2 be the largest entry value of the vector max lAy - bl using the max(abs(Ay - b)) command. Repeat this for Gauss-Seidel with Tgs_2 and Egs_2.
Repeat the entire experiment for ∈ = 1e - 4, ∈ = 1e - 6, and ∈ = 1e - 8. This will give us Tj_4, Ej_4, Tj_6, Ej_6, Tj_8, Ej_8, Tgs_4, Egs_4, Tgs_6, Egs_6, Tgs_8, and Egs_8. You’re welcome to write these in vectors Tj, Ej, Tgs, Egs instead of scalar variables if you choose to.
Set the row vectors A1, A2, A3, and A4 as A1 = [Tj_2, Tj_4, Tj_6, Tj_8], A2 = [Ej_2, Ej_4, Ej_6, Ej_8], A3 = [Tgs_2, Tgs_4, Tgs_6, Tgs_8], and A4 = [Egs_2, Egs_4, Egs_6, Egs_8].
PRoBLEM 2
Consider the following simplified scenario of the Covid-19 pandemic. We divide the entire population into three classes:
● Susceptible (S)
● Infected (I)
● Recovered/Immune (R)
The susceptible class has either not been exposed to the virus or has not been given the vaccine. The infected class will recover eventually but can infect others in the mean time. The recovered class has either had either been exposed to the virus and has recovered or has been successfully vaccinated. Lets suppose in this scenario that we do not consider the otherwise grim reality of this pandemic. We observe that it is difficult to change human behavior/interaction but suppose we can produce vaccinations. So, we study the effect of vaccination behavior of the outbreak.
Suppose today is day zero and we capture the proportion of the population in each of the classes S, I, R in a column vector
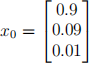
It is observed that each day 1/1, 000 of the infected individuals recover. Each day, 1 out of every 200 susceptible individuals becomes infected. Because of mutations in the virus, 1/10, 000 of the recovered individuals become susceptible again. Through vaccination, we are able to move some fraction of the individuals in S directly to R; call this fraction p where 0 5 p 5 1. Find a matrix M such that
x1 = Mx0
describes the change in the population make up from day 0 to day 1. This is the same matrix that describes the transition of the population from day k to day k + 1. Note that if some number of individuals move from one class to another, you have to remove them from the class they were in originally (the columns of your matrix M should all sum to 1).
(1) With p = 0, determine
(a) For this value of p, save the matrix as A5 = M.
(b) Which day is the first day where at least 50% of the population is infected? Call this day D0 (on Python don’t forget to add by 1).
(c) The system reaches a steady state as the number of days that have passed goes to infinity. Estimate the fraction of the population that is infected in the long term. Call this F0.
In order to prevent tolerance errors, for F0, if you use a for loop, pick a large value (say 100000) to be your final iteration, and break out of the loop only if two subsequent (absolute) values of the infected variable is less than 1e - 8.
(d) Save a row vector A6 = [D0, F0].
(2) Now suppose that we are able to successfully vaccinate 2 out of every 1000 of the susceptible people everyday; i.e., p = 2/1000.
(a) For this value of p, save the matrix as A7 = M.
(b) Which day is the first day where at least 50% of the population is infected? Call this day D1 (on Python don’t forget to add by 1).
(c) Estimate the fraction of the population that is infected in the long term. Call this F1
In order to prevent tolerance errors, for F1, if you use a for loop, pick a large value (say 100000) to be your final iteration, and break out of the loop only if two subsequent (absolute) values of the infected variable is less than 1e - 8.
(d) Save a row vector A8 = [D1, F1].
PRoBLEM 3
Consider the linear system An φ = ρ, where An is an n × n matrix with 2’s on the main diagonal, -1’s directly above and below the main diagonal and 0’s everywhere else. For example,
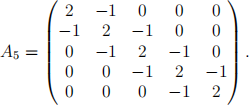
This is a discretized version of Poisson’s equation
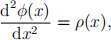
which appears very often in physical applications. We will discuss discretizations and differential equations, including the origin of the matrix An , later in the class.
(1) Setting up the matrix:
(a) Construct the matrix A114 in MATLAB/python. (You should be able to do this in only a few lines of code with the help of the diag or np.diag function. In particular, you should figure out what the commands diag(v), diag(v, 1) and diag(v, -1) do when v is a vector or 1D array.) Save a copy of this matrix in a variable named A9 (remember, in python you need to use A9 = A.copy()).
(b) Now construct the right hand side vector ρ. This should be a 114 × 1 vector such that the jth entry of ρ is

Save a copy of this vector in a variable named A10 (remember, in python you need to use A10 = rho.copy().
(2) Jacobi method:
(a) The Jacobi method for this problem can be written as φk = Mφk -1 + C, where M is a 114 × 114 matrix that we discussed in lecture. (Note that φk in this equation means the kth guess for the vector φ and it is an entire vector. It does not mean the kth entry of φ). Use the Jacobi method to solve for φ. Your initialization should be a 114 × 1 vector of all ones, and you should use a tolerance of 10-5 . That is, you should stop when max lφk - φk -1 l < 10-5 using the abs() and max() functions. Save a copy of your final iteration in a 114 × 1 column vector named A11. Save the total number of iterations required (including the initial iteration) in a variable named A12.
(b) The true solution to the system of equations Aφ = ρ is the 114 × 1 vector φ whose jth entry is defined according to the formula
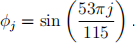
To test the efficacy of the Jacobi method on this problem, find the maximum error in absolute value between your final iteration and the true solution using the abs() and max() functions. Save your result in a variable named A13.
(3) Gauss-Seidel method:
(a) The Gauss-Seidel method for this problem can be written as φk = Mφk -1 + C, where M is a 114 × 114 matrix that we discussed in lecture. Use the Gauss-Seidel method to solve for φ. Your initial iteration should be a 114 × 1 vector of all ones, and you should use a tolerance of 10-5 . Save a copy of your final iteration in a 114 × 1 column vector named A14. Save the total number of iterations required (including the initial iteration) in a variable named A15.
(b) To test the efficacy of the Gauss-Seidel method on this problem, find the maximum error in absolute value between your final iteration and the true solution from the previous part. Save your result in a variable named A16.
2022-02-07