Data Mining and Machine Learning (2020)

Lab – Neural Networks

Problem

The challenge is to implement the Error Back-Propagation (EBP) training algorithm for a multi-layer perceptron (MLP) 4-2-4 encoder [1] using MatLab (or your language of choice). Intuitively the structure of the encoder is as shown in Figure 1.

Figure 1: MLP structure for 4-2-4 encoder

The MLP has an input layer with 4 units, a single hidden layer with 2 hidden units, and an output layer with 4 units. Each unit has a sigmoid activation function. The task of the encoder is to map the following inputs onto outputs:

Table 1: Input-output pairs for the 4-2-4 encoder

The problem is that this has to be achieved through the 2-unit “bottle-neck” hidden layer. Rumelhart, Hinton and Williams demonstrate that to achieve this, the MLP learns binary encoding in the hidden layer.

Input (and target) pattern

There are 4 input patterns, and the targets are equal to the inputs (Table 1). Recall that the output 0j of the jth unit in the network is given by:

where netj is the input the jth unit. The values of oj converge towards 0 and 1 as the magnitude of netj becomes large, but the values 0 and 1 are never realised. Hence for practical purposes it is better to replace, for example, 1, 0, 0, 0 in Table 1 with 0.9, 0.1, 0.1, 0.1.

Since there are only these 4 input/output pairs, the training set consists of just 4 input/output pairs.

Structure of the program

The program needs to run the EBP weight updating process multiple times. So you will need a variable N for the number of iterations and an outer loop (for n=1:1:N). You could terminate the process when the change in error drops below a threshold but this is simpler for the moment. In addition you will need a second inner loop (for d=1:1:4) to cycle through the 4 input patterns in each iteration. But before you do this you need to set up some basic structures:

    You will need two arrays W1 and W2 to store the weights between the input and hidden, and hidden and output layers, respectively. I suggest that you make W1 of size 4x2 and W2 of size 2x4. You will need to initialize these arrays (randomly?). Given an output x from the input layer, the input y to the hidden layer is given by:

y = W1’*x;

Note the transpose!

    The output from the hidden layer is obtained by applying the sigmoid function to y, so you will need to write a function to implement this function.

    Once you have propagated the input to the output layer you can calculate the error. In fact the only use you have for the error is to plot it to help confirm that your code is working.

    Now you need to back-propagate to calculate &j for every unit j in the output and hidden layers. First you need to calculate &j for every output unit (see equation (12) in the slides). Then you need to apply back-propagation to calculate &j for every hidden unit (again see equation (12) in the slides). To back-propagate the vector of &js from the output layer to the hidden layer you just need to multiply by W2 (no transpose this time):

deltaH = W2*deltaO;

where deltaO and deltaH are the deltas in the output and hidden layers, respectively.

Once you have calculated the &js for the output and hidden layers you can calculate

(see slide 12 from the lecture)

    Finally, you can update the weights:

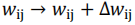
I suggest you do all this about 1,000 times (n=1:1:N, N=1000) and plot the error as a function of n.

Practical considerations

If you implement all of this properly you will see that the error decreases as a function of n. You should play with the learning rate, different initialisations of the weight matrices, different numbers of iterations etc. However, you will find that whatever you do you cannot get the error to reduce to zero. To do this I think you need to add bias units to the input and hidden layers.

Lab-Report Submission

Submit your source code and comments on experimental evaluations and results obtained.

References

[1] D. E. Rumelhart, G. E. Hinton, and R. J. Williams (1986), “Learning Internal Representations by Error Propagation”, In: Rumelhart, D.E., McClelland, J.L. and the PDP Research Group, Eds., Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations, MIT Press, Cambridge, MA, 318-362.