Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MATH  314 THE  SYMMETRIC  GROUP

HOMEWORK  1

Problem 1. Consider Z(N) = {0, 1, ..., N - 1}.  Suppose χ :  Z(N) → C \ {0} is a function such that

χ(m + n) = χ(m)χ(n)   for all m, n e Z(N).

Show that we must have χ = ee  for some l = 0, 1, 2, ..., N - 1.

(Hint: first show χ(0) = 1.  Then determine what values are possible for χ(1) .

Problem 2. a) For ee1    and ee2    instances of the functions we have defined on Z(N), find a

simple formula for

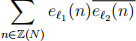
in terms of l)  and l1 . (Recalling ee (n) = ei1πen/N  may be helpful.)

b) Prove for f, g : Z(N) → C,

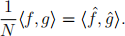
Problem 3. Let σ be the permutation 3 4 5 2 1 (in one line notation), and let τ be the permu- tation 5 3 2 4 1. Write the following permutations in cycle notation: σ, τ, σ 1 , στ, τσ .

Problem 4. Prove that sn  is generated by the n - 1 transpositions (1 2), (1 3), ..., (1 n).

Problem 5. Use one-line notation to write a permutation π = x) x1  . . . xn  e sn . An inversion is a pair of (xi , xj ) such that i < j and xi   > xj .  Let inv[π] be the number of inversions of π.  (So for instance 3 4 5 2 1 has inversions (3, 2),  (3, 1),  (4, 2),  (4, 1),  (5, 2),  (5, 1),  (2, 1) and inv[3 4 5 2 1] = 7.)

a) Show that if π can be written as a product of k transpositions, then k 三 inv[π] (mod 2).

b) Show that the sign of a permutation π is well-defined.