COM00013C Theory 1 2021–22
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COM00013C
BSc, BEng and MEng Degree Examinations 2021-22
Computer Science
Theory 1
Section A: Counting
(9 marks)
![]()
![]() Suppose that you have three bananas, four apples and five pears in a fruit bowl. You wish to select two pieces of fruit for your packed lunch.
Suppose that you have three bananas, four apples and five pears in a fruit bowl. You wish to select two pieces of fruit for your packed lunch.
[2 marks] How many ways are there of doing this if there are no constraints on the
selection i.e. the two pieces of fruit may be the same or may be different?
[4 marks] How many ways of doing this are there if the two pieces of fruit must be of
different types?
[3 arks] Coent on the relationship bet een your t o ans ers in parts (i) and (ii) above.
(6 marks)
Consider the set of natural numbers from 1 to 100, S = {1,2 ... 100}. To determine the number of elements, Nx, that are multiples of a certain natural number, x, we can use
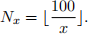
|
Similarly, to determine the number of elements that are simultaneously multiples of n numbers, we have |
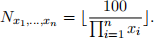
where the capital pi sign (H)indicates that we take the product of the n numbers x《.
By using the above expressions and the principle of inclusion-exclusion, determine the number of members of the set, S, that are multiples of 2, 3 or 5. You should show all of your working, with clear labelling of any sets that you wish to define and their cardinalities.
Section B: Discrete probability
3 (8 marks)
Tennis ,player A is known to get an ‘ace' serve 10% of the time when playing against tennis ‘player B'. You may assume that tennis player A serves 50 times in a set against player B.
(i) [2 marks] What is the probability that playerA hits exactly five aces in the set?
(ii) [4 marks] What is the probability that player A serves five or fewer aces in the set?
(iii) [2 marks] What is the probability that playerA serves six or more aces in the set?
4 (7 marks)
A test for an infectious disease is not completely accurate. For people who have the disease, 95% of them return a positive test. For people who do not have the disease 10% of them return a positive test. Suppose that, in a certain city, 30% ofthe population have the disease.
(i) [2 marks] Write down the two probabilities P(D),P(D), which are prior probabilities, of a
person having the disease and not having the disease respectively.
(ii) [2 marks] Write down the two probabilities P(T|D), P(T|D), which are the conditional probabilities (likelihoods), that a person tests positive for the disease, when they have the disease and don't have the disease, respectively.
(iii) [3 marks] A person from this city is selected at random and tested, with a positive test. Use Bayes' theorem to determine the probability that the person has the disease. You must show all your working and use symbols consistent with parts (i) and (ii) above.
Section C: Graphs
(7 marks)
This question refers to the graph in Figure 1.
|
|
|
|
|
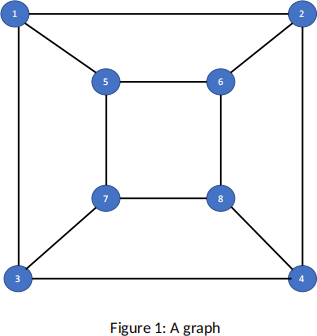
(i) [1 mark] What is the order of the graph, and the size of the graph?
(ii) [1 mark] Write down the degree sequence of the graph.
(iii) [2 marks] Write down the last row of the distance matrix for the graph with the same row and column ordering as the graph’s numerical vertex labels.
(iv) [1 mark] What is the diameter of the graph?
(v) [1 mark] How many cycles does the graph have where 4 distinct vertices are visited? (In your answer treat cycles that use the same edges, but in a difffferent order, as distinct cycles.)
(vi) [1 mark] Provide an example of a Hamiltonian cycle in the graph.
6 (13 marks)
This question refers to the graph in Figure 1 from the previous question.
Suppose now that ,distance' weights are applied between any pair of vertex indices, (i,j), such that:
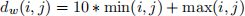
where the functions min and max return the minimum and maximum of their argument lists respectively.
(i) [1 mark] Copy the diagram in Figure 1 and add the distance weights as labels to the edges of the graph.
(ii) [6 marks] Using vertex 1 as the starting vertex, use Djikstra's algorithm to find the shortest path to vertex 8. Use the table below to add distance values from the start vertex in order to work through the algorithm in the manner demonstrated in the lectures and problem sheets.

Table 1: TableforDjikstra'salgorithm: i are the indices of the vertices, and d(i) are theestmnated distances of the vertices to the start vertex. The edge column reports the most recent edge used to update the vertex distance estimate. The final row, marked ,current vertex' is used to report the index of the current vertex (i.e. the currently ,visited' vertex)
(iii) [2 marks] For each vertex, give the lowest distance from the start vertex determined by the
algorithm. This should be a list of eight numbers, corresponding to vertices 1to8 respectively.
(iv) [2 marks] Give the order in which the vertices are visited in the algorithm.
(v) [2 marks] Give the shortest path vertex sequence, from the start vertex to the destination
vertex.
Section D: Logic.
7 (8 marks)
(i) [4 marks] Re-express ((p 今 q) A (r 今-q))今(p 今—r) as a formal argument. Demonstrate the validity or invalidity of the argument by constructing a truth table and making a statement about its contents.
(ii) [4 marks] State the translation rule equivalence for p 今 q and use it to show that F 今 p, p 今 p, and p 今 T are all TRUE.
Section E: Sets and Inductive Arguments.
8 (10 marks)
(i) [2 marks]
Let M = {Ham, Egg, Milk, Bread, Cheese, Apple,Yoghurt, Juice}. Write down the set P, by selecting any valid combination from the following five subsets of M, such that P is a partition of M.
Ma = {Egg, Bread, },
Mb = {Milk, Cheese, Ham,Yoghurt},
Mc = {Egg, Ham, Milk, Bread}.
Md = {Juice, Apple},
Me = {Ham, Cheese, Apple,Yoghurt, Juice}
(ii) [4 marks] Consider the statement: Pn,(n e Z+ 今 nn < 22n) where Z+ is the set of positive integers.
(a) [1 mark] Why would a single counterexample disprove this statement?
(b) [3 marks] Confirm this by giving a suitable counterexample.
(iii) [4 marks] For the following statements, the universal set is given as
U = {0,1, 2,3,4, 5,6, 7,8,9,10}. If x e P and y e Q, then define the two sets P and Q that satisfy each of the following statements:
(a) [1 mark] Bx, 'iy, (x + y > 5)
(b) [1 mark] Fx, By, (x — y < 0)
(c) [2 marks] Bx, By, ((x : y) e z) A (x + y = 4))
Section F: Functions and Relations.
9 (8 marks)
Let A represent a set of 100 adults in a dietary trial and let D be the set of all defined diets in the trial.
Given that the relation A o D represents the concept: ‘adult person on a dietary restriction', the following conditions apply:
• In the group, every adult can opt in to having only one of four dietary restrictions (Vegan, Vegetarian, Pescatarian, Gluten-free).
• 50% of the adults in the group have chosen one of the four dietary restrictions.
• All four dietary choices have been chosen by someone.
For the relation A o D, state whether each of the following properties applies to the defined relation, highlighting which of the defined conditions relates to that conclusion, or else giving a reason if none applies.
(i) [2 marks] a function
(ii) [2 marks] injective
(iii) [2 marks] surjective
(iv) [2 marks] reflexive
(i) [4 marks] This part refers to the digraph shown in Figure 2, which defines a relation, R.
|
|
|
|
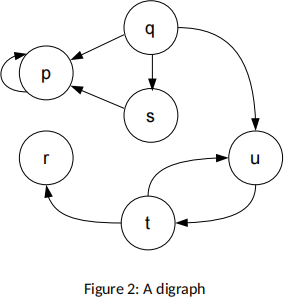
(a) [2 arks] rite do n R as a set of ordered pairs.
(b) [2 marks] Write down the adjacency matrix for R.
(ii) [3 marks] Let D = {(2,2), (2,4), (2, 7), (4, 4), (4, 7), (7,4)} be a relation on the set
{2,4, 7}. List the set of ordered pairs, of minimal cardinality, that is needed to be added or removed to make D:
(a) [1 mark] reflexive
(b) [1 mark] symmetric
(c) [1 mark] anti-symmetric.
(iii) [1 mark] For the same relation D, given in part (ii), if all reflexive pairs are removed, would the relation be transitive?
Section G: Ordering and Equivalence.
11 (8 marks)
(i) [5 marks] The relation > is defined on the set P = {6,9,15, 54, 78,90} by the rule: ni > n exactly if (n = (6 x ni)) V (ni = &).
(a) [2 marks] Draw a Hasse diagram for the relation > on P.
(b) [3 marks] State whether the relation > on P is an ordering or not. Explain your conclusions based upon the relation's adjacency matrix, or other reasoning.
(ii) [3 marks] Let R = {(a, a), (a, b), (a, d), (b, a), (d, a), (d, b)} be a relation on the set {a, b, d}.
(a) [2 marks] Determine the adjacency matrix of R+, where R+ is the transitive closure of R.
(b) [1 mark] List the relation R+ as a set of ordered pairs.
12 (4 marks)
A set, S, represents a fleet of company-owned cars with a cardinality of #S = 275. Let subset P represent cars able to run on petrol, D represents cars able to run on diesel, and E represents cars able to run on electric. The following information is known about the cars:
• 120 of them can run on petrol, 75 can run on diesel, 50 can run on electric.
• 9 cars can run on petrol and diesel.
• 4 cars are petrol/electric hybrids.
• 51 cars are diesel/electric hybrids.
• 1 car can use all three fuel/power options.
Determine how many cars there are that do not use petrol, diesel, or electric power options.
(a) [3 marks] Given a set of animals, A = {dog, cat, rat, mouse}, write down the largest subset, P, of the powerset 2A, such that
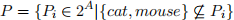
(b) [1 mark] List the elements of the power set of A that are excluded from P.
2022-01-17