MATH375 Class Test 2 Solutions
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH375 Class Test 2 Solutions
In all questions below (W (t), t >) is a standard Brownian motion and (F(t), t > 0) is its natural filtration.
1. Use Itˆo’s formula to show that:

with a e R, is the solution to the equation
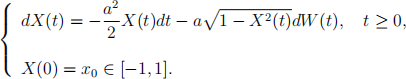
Solution. By Itˆo’s formula, the differential of X(t) is:
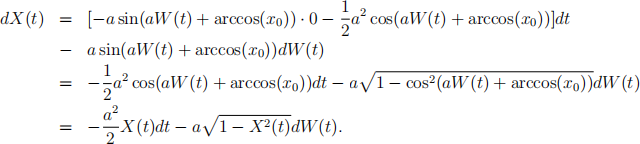
Since X(0) = cos(aW (0) + arccos(x0 )) = cos(arccos(x0 )) = x0 , we conclude that X(t) := cos(aW (t)+arccos(x0 )) is the solution to the given stochastic differential equation.
2. Consider the following equation:
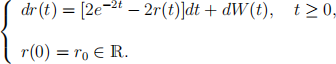
(i) Find the solution (r(t), t > 0).
(ii) Find E[r(t)], t > 0.
(iii) Does this equation have the mean-reverting property? Justify your an- swer.
Solution. (i) The solution to this equation is:
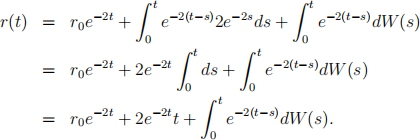
(ii) The expected value of solution is:
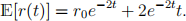
(iii) The mean-reverting property is concerned with the following limit:
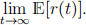
If this limit converges to a certain value for all r0 , then we say that the equation has the mean-reverting property. In the given case we have:
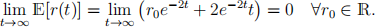
Thus, the equation has the mean-reverting property.
3. Consider the following stochastic differential equations:
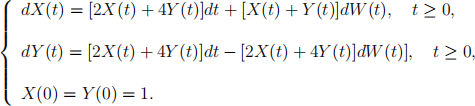
Using Itˆo’s product rule, find the differential of Z(t) := X(t)Y (t). Is the process Z(t) a martingale with respect to (F(t), t > 0)? Justify your answer. [10 marks]
Solution. By Itˆo’s product rule, the differential of Z(t) := X(t)Y (t) is:
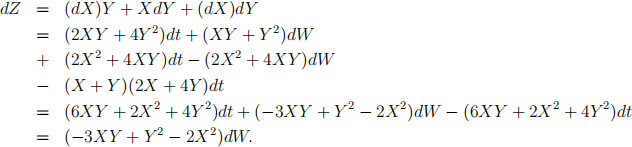
Integrating both sides from 0 to t gives:
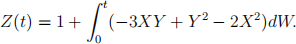
Since Z(t) is a constant plus a stochastic integral, then it is a martingale as so is the stochastic integral.
2022-01-17