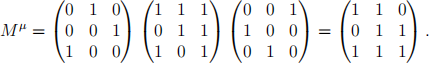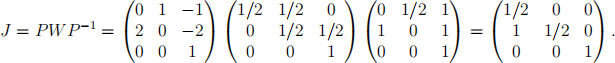Solutions - MA3604 Discrete Mathematics - 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Solutions - MA3604 Discrete Mathematics - 2021
1. (a) i. The adjacency matrix corresponding to the labelled graph is
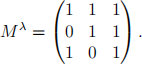
For an adjacency matrix M the entry (Mn )ij is the number of paths of length n starting at vertex λ(i) and ending at vertex λ(j) in the corresponding labelled
graph. Taking n = 5 in our case we find
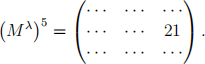
Thus there are twenty-one paths of length five starting at vertex-2 and ending at vertex-3.
ii. The same graph labelled under µ is
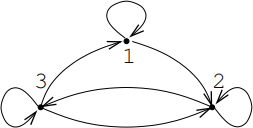
and the new adjacency matrix is

Writing µ(i) = λ(P (i)), then P is the permutation
P (1) = 2, P (2) = 3, P (3) = 1.
Let U be the permutation matrix with entries Uij = δi,P (j):
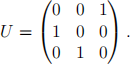
We write Mµ for the adjacency matrix of the same graph, now with vertices labelled according to µ. It was shown during the Course that Mλ = UT Mλ U . Then
This agrees with the adjacency matrix found in part b).
(b) The i-th diagonal entry of M达 is Mij Mji (sum over j implied). For each j, this is the number of edges from vertex i to vertex j, times the number of edges from vertex j back to vertex i. The sum over j gives the total number of paths of length 2 starting
and finishing at vertex i
If (M达 )ii is zero, there are no paths of length 2 starting and finishing at vertex i. That is, if there is an edge from vertex i to some other vertex j, then there is no edge from j back to i.
2. (a) The transition matrix is
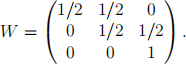
Stationary states (x, y, 1 ì x ì y) are left eigenvectors of W having eigenvalue 1. Therefore
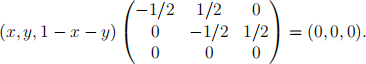
The only solution to this is x = y = 0. Therefore the sole stationary state of the
given graph is (0, 0, 1).
(b) Start by finding the spectrum of W . Its characteristic polynomial is (1/2 ì x)达 (1 ì x), so that the eigenvalues of W are 1/2, having algebraic multiplicity two, and 1, of multiplicity one. Next we find the eigenvectors associated with eigenvalue 1/2.
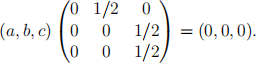
A basic solution to this is u(|) = (0, 1, ì 1), and there are no more independent eigenvectors associated to eigenvalue 1/2.
(Note: It is possible to deduce the Jordan form of W at this stage, but if this is done and in particular the matrices P and P一| below are not given then only five marks shall be awarded for the rest of this sub-question.)
Note that u(|) ← Im /W ì 达(|) I、 and therefore has a “predecessor” u(达) such that /W ì达(|) I、u(达) = u(|), which we find next.
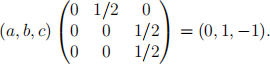
All solutions of this are of the form (2, b, ìb ì 2) = (2, 0, ì2) + b u(|) .
It is best to choose “predecessors” having no part in Ker (W ì λ I), where λ is the eigenvalue being considered. Thus we choose b = 0 and thus u(达) = (2, 0, ì2). [3] Because u(达) ![]() Im /W ì达(|) I、it has no predecessors of its own and we are done with eigenvalue 1/2.
Im /W ì达(|) I、it has no predecessors of its own and we are done with eigenvalue 1/2.
As for eigenvalue 1, we already found eigenvector u(|)╱ = (0, 0, 1), which is not in
Im (W ì I) and so has no predecessors. Thus we are done with eigenvalue 1. [1]
The matrix that effects a change of basis from the original one to the ordered vector
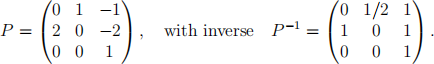
|
The Jordan form of W is
|
As discussed during the Course, a Jordan block carrying an eigenvalue of modulus less than one converges to a zero matrix upon raising it to increasingly higher powers. Therefore
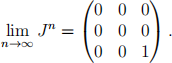
(c) It follows from the above that
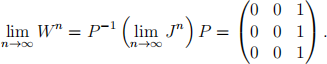
Calling this limit W& , any initial state (x, y, 1 ì x ì y) will converge under time evolution to the state (x, y, 1 ì x ì y)W& .
In our case
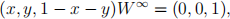
as was to be expected, (0, 0, 1) being the only stationary state of the graph.
3. Not currently examinable
4. (a) The degree formula for faces gives 3 F& + 4 F) = 2|ε|, in which Fn is the number of faces of degree n. The degree formula for vertices gives |ε| = 2|V |.
Substitution of these into the Euler formula, with |F | = F& + F), results in
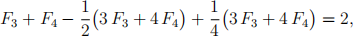
which simplifies into F& = 8.
(b) By the degree formula for faces, the average degree face is f¯ = 2|E|/|F |. For a trivalent graph 2|E| = 3|V |, and because the graph is planar and connected we have also the Euler formula |V | ì |E| + |F | = 2. Combining these formulas we find that
f¯ = 6 ì 12/|F |.
The larger a graph of this kind is, the larger |F | becomes, and f¯ tends to 6.
(c) i. This graph has six vertices, each of degree three. Because all vertices of K扌 have degree four, no subdivision of K扌 may be a subgraph of it.
Note that the vertices that lie in alternating positions on the hexagon are never connected to each other, and that each one of these is connected to each of the three other vertices. Therefore the graph is complete bipartite, and in fact it is
identical to K&,& , which is known not to be planar.
ii. K扌 can be ruled out as a subgraph because there aren’t five vertices of degree four. In fact, all eight vertices have degree three, It is possible that K&,& or a subdivision of it may be a subgraph.
If one of the short diagonal edges is removed, the resulting graph is a subdivision of K&,& . Therefore the original graph contains a subgraph that is a subdivision of K&,& . By the Kuratowski theorem, the original graph admits no planar rep- resentations.
2022-01-15