MA3604: Discrete Mathematics 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MA3604
Discrete Mathematics
2021
1. (a) Consider the directed graph shown below, in which the vertices have been numbered according to a certain labelling λ .
i. [5] Give its adjacency matrix Mλ and use it to calculate the number of paths of length five which start at vertex-2 and end at vertex-3.
ii. [15] Let µ be a labelling of the same graph such that λ(1) = µ(3), λ(2) = µ(1) and λ(3) = µ(2). Give a representation of the graph with labelling µ, and find the adjacency matrix Mµ . Find the similar- ity transformation which relates Mµ and Mλ and show how Mµ is obtained from Mλ .
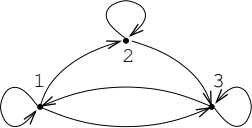
(b) [10] Let M be the adjacency matrix of a loop-free directed graph. If all the diagonal entries of M2 are zero, what can we deduce about the graph?
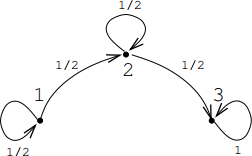
2. Let G be the weighted graph shown below.
(a) [5] Give its transition matrix W and find its stationary states.
(b) [15] Find the Jordan form of W . Based on your result, decide if Wn converge as n tends to infinity.
(c) [10] Use your results to decide whether any initial state defined on G will converge to a stationary state as it evolves forwards in time. If yes, deduce the state to which any initial state will converge. If not, give an example of an initial state whose time evolution is not convergent.
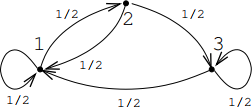
3. Consider the weighted graph shown below.
(a) [15] Find the probability that a random walk on this graph which starts at vertex-1 will return to it in exactly n steps.
(b) [5] Based on your result, decide whether every random walk on this
graph which starts at vertex-1 will eventually return to it.
(c) [10] If the answer to the previous question is yes, calculate the average number of steps after which a random walk starting at vertex-1 will return to it. If the answer is no, then give an example of a random walk that starts at vertex-1 but may not return to it.
4. (a) [10] A non-empty connected planar graph has vertices of degree four only, and faces of degree three or four. Find the number of faces of degree three.
(b) [10] The average face degree of an undirected planar graph is defined as 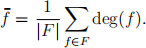 Give an expression for the average face degree of
Give an expression for the average face degree of
a trivalent connected planar graph (one whose vertices all have degree three) in terms of its number of faces. Then show that all sufficiently large graphs of this kind have approximately the same average face degree.
(c) For each of the following graphs, use the Kuratowski theorem to decide whether an equivalent planar representation exists (you don’t need to state the theorem.)
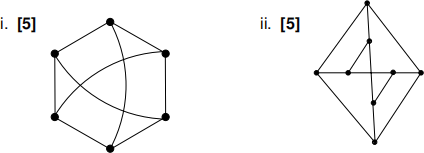
![]()
![]()
![]()
![]()
![]()
2022-01-15