COMP4019 - Lab Session 9 – Mockup Exam
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
COMP4019 - Lab Session 9 – Mockup Exam
1 Amortized Analysis
1.1 Potential Functions
Note: This is one is just a warm-up on the potential method and an excuse to think about trees.
Consider a tree data structure t. We note:
● r the root of t
● n(x) the number of nodes in the subtree rooted at x
● h(x) the height of a node x
● dlow and dhigh , the minimum and maximum depths of leaves
Among the following options, mark which potential functions are valid (note that since you do not know the structure of t or the algorithm performed on it, you cannot know which ones if any make sense to perform amortized anal- ysis, only whether they are valid or not). Argue why/why not. Determine the potential of an empty tree for each.
1. φ 1 (t) = n(r)2
2. φ2 (t) = dlow 一 dhigh
3. φ3 (t) = h(r) 一 dlow
4. φ4 (t) = 2h(r) 一 n(r)
1.2 Move To Front
Note: This is not an easy application of amortized complexity, but I am running out of “simple/self-contained” examples to illustrate the concept. It is an inter- esting and different application of it nonetheless, and one in which the aggregate method does not work.
Linked lists are notorious for having bad complexity for random accesses. To address this shortcoming, one approach is that of self-organizing lists. The idea of self-organizing lists is that the nodes in the list are dynamically rearranged based on how frequently they are accessed (it is thus in some way related to the concept of consolidation)
Move to front (MTF) is a heuristic technique for self-organizing lists that consists in moving an element to the front of the list when it is accessed. For instance, accessing D in the following list has the indicated effect:
(A, B, C, D, E, F) → (D, A, B, C, E, F)
The complexity of these accesses can be compared to that of an “idealized” heuristic. Consider a heuristic IDL that knows in advance in what order ele- ments will be accessed, and has the ability to reorder the list once (for free) before starting these accesses. The IDL heuristic does not reorder the list after each find operation (although it can further be shown that this does not change the result below).
Show that the amortized cost of findMTF in a singly-linked list is within a constant multiplicative factor of that of findIDL .
1. Start by finding a potential function that captures the difference in poten- tial between a list ordered according to MTF and one according to IDL. Both heuristics are given an identical list (thus the potential must be 0), then IDL performs a free one-time re-ordering, then find operations may be performed and their cost analyzed.
2. Compute the change in your potential function after executing a find operation in MTF and in IDL.
3. Show the stated bound.
2 Graphs
Note: Graph stuff. Good exercise to test your understanding on graphs, and manipulate formal definitions and statements on them.
The edge-to-vertex dual of an unidrected graph G = (V, E) is an undirected graph G# = (V# , E# ) such that:
● V# = E;
● E# = {(ei , ej ) ∈ E2 l ei ![]() ej and a v ∈ V : v ∈ ei A v ∈ ej }.
ej and a v ∈ V : v ∈ ei A v ∈ ej }.
In other words: for each edge in G there is a vertex in G# ; and for every two edges in G that share a vertex, there is an edge between their corresponding vertices in G# . Below is an example of a graph G (left) transformed into its edge-to-vertex dual G# (right).
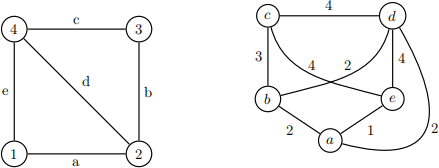
1. Write (in pseudocode) a “edge-to-vertex dual” conversion algorithm e2v convert.
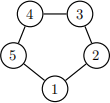
2. Show that if G is a cycle graph (a graph consisting of a single cycle – see example below), the edge-to-vertex dual conversion is isomorphic (that is,
the resulting graph is identical, up to relabeling of the nodes and vertices).
Example of a cycle graph:
3 Trees
Note: Tests simple algorithms on trees and your ability to reason about trans- formations. Inspired by a Google coding interview question.
Consider a ternary tree t. Each node has left, middle and right children (some potentially empty).
1. Write (in pseudocode) the mirror operation that swaps the left and right children for each subtree of a tree t.
2. Write (in pseudocode) the lflush operation that flushes children towards the left, such that any empty child pointer is replaced by the pointer to its right.
3. Show that lflush(mirror(t)) = lflush(mirror(lflush(t))). Hint:
consider each level independently.
An example of the two operations in action (if a node has three empty children, the pointers are not shown):
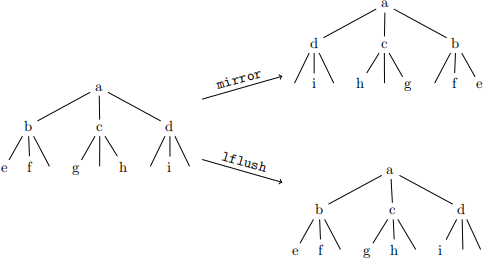
4 Dynamic Programming
Note: Tests your understanding of the usability of dynamic programming.
For each of the following problem statements, determine whether (1) it demonstrates optimal substructure and whether (2) it possesses overlapping sub- problems. Briefly explain why or why not for both.
1. Computing Fn , the n-th Fibonacci number recursively (reminder: Fn = Fn − 1 + Fn −2 and F0 = 0, F1 = 1);
2. Binary search for a given key in a sorted array;
3. The rod-cutting problem (reminder: given a rod of length n and a table of prices p1 , . . . , pn for pieces of lengths 1, . . . , n, cut the rod into pieces maximizing the total price);
4. Variant on the rod-cutting problem where each “cut” has a given fixed cost c;
5 Mysterious Algorithm
Note: Algorithm complexity analysis. Should be fairly straighforward. Be mind- ful about what is/are the “variable(s)” here.
Consider the following pseudocode of an algorithm on arrays:
function MysTERy (A, a, b, k)
if a = b then
return A[a]
c ← AUxILIARy(A, a, b)
if k = c then
return A[k]
else if k < c then
return MysTERy (A, a, c 一 1, k)
else
return MysTERy (A, c + 1, b, k)
Random accesses are in Θ(1). The AUxILIARy function runs in O(b 一 a), and returns c such that a ≤ c < b. Determine (and justify) the worst-case complexity of MysTERy (A, 0, n 一 1, k).
2022-01-07